陕西省宝鸡市凤翔区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算中，结果正确的是（）

A、 $x^{3} \cdot x^{3} = x^{6}$ B、 $3 x^{2} + 2 x^{2} = 5 x^{4}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
2. “翻开人教版《数学》九年级上册课本恰好翻到第 $56$ 页”这个事件是（）

A、随机事件 B、确定事件 C、不可能事件 D、必然事件

查看试题解析
3. 将英语单词“LOVE”的每一个字母都看成一个图形，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 某人要在规定的时间内加工100个零件，如果用 $n$ 表示工作效率，用 $t$ 表示规定的时间，下列说法正确的是（）

A、数100和n,t都是常量 B、数100和n都是变量 C、n和t都是变量 D、数100和t都是变量

查看试题解析
5. 小华把如图所示的4×4的正方形网格纸板挂在墙上玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等），则飞镖落在阴影区域的概率是（）

A、 $\frac{3}{16}$ B、 $\frac{1}{4}$ C、 $\frac{5}{16}$ D、 $\frac{7}{16}$

查看试题解析
6. 如图，在等腰 $Δ A B C$ 中， $A B = A C$ ， $∠ A = 40 °$ ， BD是 $∠ A B C$ 的角平分线，则 $∠ A D B$ 的度数等于（）

A、 $70 °$ B、 $100 °$ C、 $105 °$ D、 $120 °$

查看试题解析

7. 某剧院观众的座位数按下列方式设置：

排数（x）	1	2	3	4	…
座位数（y）	30	33	36	39	…

根据表格中两个变量之间的关系，当 $x = 8$ 时y的值为（）

A、49 B、51 C、53 D、55

查看试题解析

8. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D是BC边的中点，连接AD，点P在AD上，连接BP，CP，过点D作 $D E ⊥ B P$ ， $D F ⊥ C P$ ，垂足分别为E、F，则下列结论：① $B D = C D$ ；② $△ B D E ≌ △ C D F$ ；③ $D E = P E$ ；④ $△ B C P$ 是等腰三角形．其中正确的有（）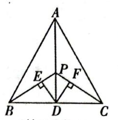

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 已知a^m＝2，aⁿ＝3，则a^m+n的值为 .

查看试题解析
10. 变量x与y之间的关系式是 $y = - x + 1$ ，当自变量 $x = 2$ 时，因变量y的值是．

查看试题解析

11. 绿化公司对某种花苗移植的成活率进行调查，结果如表所示：

移植总数（n）	400	750	1500	3500	7000	9000	10000
成活数（m）	369	662	1335	3203	6335	8073	9013
成活的频率 $\frac{m}{n}$	0.923	0.883	0.890	0.915	0.905	0.897	0.901

根据表中数据，估计这种花苗移植的成活概率为．（精确到0.1）

查看试题解析

12. 如图，AD是 $△ A B C$ 的中线， $A C = 6 cm$ ， $A B = 4 cm$ ，且 $△ A B D$ 的周长为11cm，则 $△ A C D$ 的周长是cm．

查看试题解析
13. 已知：四边形ABCD中，AB=AD=CD，∠BAD=90°，三角形ABC的面积为1，则线段AC的长度是.

查看试题解析

三、解答题

14. 计算： $- 1^{2022} - (\frac{1}{2})^{- 1} + (3 - π)^{0} + | - 3 |$

查看试题解析
15. 已知 $x = 2 ， y = - 1$ ，求 $[(x - 2 y) (x + y) - (x - 2 y) (x + 2 y)] \div (- 2 y)$ 的值.

查看试题解析
16. 如图， $△ A B C$ 中，用尺规作图法在AC上作一点D，使得 $∠ A B D = ∠ C$ ．（保留作图痕迹，不用写作法）

查看试题解析
17. 如图， $E F ∥ A D$ ， $∠ 1 = ∠ 2$ .则 $∠ C G D$ 与 $∠ C A B$ 相等吗？请说明理由.

查看试题解析
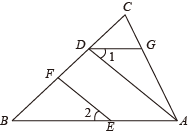18. 在一个不透明的口袋里装有4个白球和6个红球，它们除颜色外完全相同．

(1)、事件“从口袋里随机摸出一个球是绿球”发生的概率是；

(2)、事件“从口袋里随机摸出一个球是红球”发生的概率是；

(3)、从口袋里取走x个红球后，再放入x个白球，并充分摇匀，若随机摸出白球的概率是 $\frac{4}{5}$ ，求x的值．

查看试题解析
19. 如图， $△ A B C$ 的顶点在正方形网格的格点上．

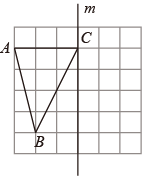(1)、画 $△ D E F$ ，使它与 $△ A B C$ 关于直线m对称；

(2)、如果在网格内任意找一点，这个点在 $△ A B C$ 和 $△ D E F$ 外的概率是多少？

查看试题解析
20. 如图1，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图2，伞圈D沿着伞柄AP滑动时，总有伞骨 $B D = C D$ ， $A B = A C$ ，从而使得伞柄AP始终平分同一平面内两条伞骨所成的 $∠ B A C$ ．请你说明其中的理由．

查看试题解析
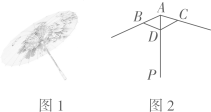21. 如图，在△ABC中，AF平分∠BAC交BC于点F，AC的垂直平分线交BC于点E，交AC于点D，∠B＝60°，∠C＝26°，求∠FAE的度数．

查看试题解析
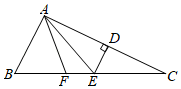22. 如图，某区有一块长为 $(3 a + 4 b)$ 米，宽为 $(2 a + 3 b)$ 米的长方形地块，规划部门计划将阴影部分进行绿化，中间的边长为 $(a + b)$ 米的空白的正方形地块将修建一个凉亭．

(1)、用含有a ， b的式子表示绿化总面积．

(2)、若 $a = 4$ ， $b = 3$ ，求出此时的绿化总面积．

查看试题解析
23. 如图，在长方形 $M N P Q$ 中， $M N = 6 ， P N = 4$ ，动点R从点N出发，沿 $N \to P \to Q \to M$ 运动至点M处停止．设点R运动的路程为x ，三角形 $M N R$ 的面积为y ．

(1)、当 $x = 3$ 时， $y =$ ；当 $x = 12$ 时， $y =$ ；当 $y = 6$ 时， $x =$ ；

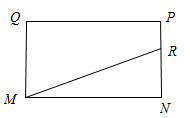(2)、分别求当 $0 < x < 4 ， 4 \leq x \leq 10 ， 10 < x < 14$ 时，y与x的关系式．

查看试题解析
24. 如图，某公园有一个人工湖，王平和李楠两人想知道这个人工湖的长度 $A B$ ，但无法直接度量，于是他们准备用所学知识，设计测量方案进行测量．已知 $B P$ 为垂直于 $A B$ 的一条小路，且小路两侧除人工湖所占区域外，其他区域均可随意到达，他们两人所带的测量工具只有一根足够长的皮卷尺，请你帮王平和李楠两人设计一种测量方案：

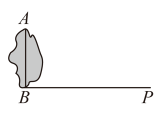(1)、请在图中画出测量示意图并写出测量数据（线段长度可用 $a$ 、 $b$ 、 $c$ ……表示）；（不要求写出测量过程）

(2)、根据你的测量方案数据，计算出这个人工湖的长度 $A B$ ．

查看试题解析
25. 如图，端午节期间，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定顾客每购买200元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针对准红、黄、绿的区域，顾客就可以分别获得50元、20元、10元的奖金，对准无色区域则无奖金（转盘被等分成16个扇形）．

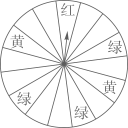(1)、王老师购物210元，他获得奖金的概率是多少？

(2)、张老师购物370元，他获得20元奖金的概率是多少？

(3)、现商场想调整获得10元奖金的概率为 $\frac{1}{4}$ ，其他金额的获奖率不变，则需要将多少个无色区域涂上绿色？

查看试题解析
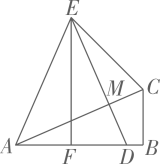26. 如图，在 $Rt △ A B C$ 和 $Rt △ E F D$ 中， $∠ A B C = ∠ E F D = 90 °$ ， $A C = E D$ ， $A C ⊥ E D$ ，垂足为M，连接EA．

(1)、 $△ A B C$ 与 $△ E F D$ 全等吗？为什么？

(2)、若 $∠ A E F = ∠ D E F$ ，判断 $∠ A E C$ 与 $∠ A C E$ 的数量关系，并说明理由．

查看试题解析