陕西省宝鸡市凤翔区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形体现了中华民族的传统文化，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{1}{x + 2}$ 有意义，则实数x的取值范围是（）

A、 $x \geq 2$ B、 $x < - 2$ C、 $x \neq - 2$ D、 $x = - 2$

查看试题解析
3. 把多项式x²+ax+b分解因式，得（x+1）（x-3）则a ， b的值分别是（）

A、a=2，b=3 B、a=-2，b=-3 C、a=-2，b=3 D、a=2，b=-3

查看试题解析
4. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在 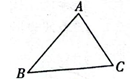$△ A B C$ （）

A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处

查看试题解析
5. 将分式 $\frac{x^{2} y}{x - y}$ 中的x，y的值同时扩大为原来的3倍，则分式的值（）

A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍

查看试题解析
6. 如图，在△ABC中，AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）

A、2 B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
7. 近日，教育部正式印发《义务教育课程方案》，将劳动从原来的综合实践活动课程中完全独立出来，并在今年9月份开学开始正式施行．某学校组织八年级同学到劳动教育基地参加实践活动，某小组的任务是平整土地 $300 m^{2}$ ．开始的半小时，由于操作不熟练，只平整完 $30 m^{2}$ ．学校要求完成全部任务的时间不超过3小时，若他们在剩余时间内每小时平整土地 $x m^{2}$ ，则x满足的不等关系为（）

A、 $30 + (3 - 0.5) x \leq 300$ B、 $300 - 30 x - 0.5 \leq 3$ C、 $30 + (3 - 0.5) x \geq 300$ D、 $0.5 + 300 - 30 x \geq 3$

查看试题解析
8. 如图，AD是 $△ A B C$ 的角平分线，DE⊥AC，垂足为E， $B F ∥ A C$ 交ED的延长线于点F，若DE＝DF，AE＝2BF．下列四个结论：①BC平分∠ABF；② $E F ∥ A B$ ；③AD⊥BC；④AB＝3BF．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 分解因式： $a^{2} - 5 a =$ ．

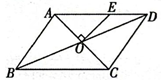
查看试题解析
10. 一个多边形的内角和与外角和的和是 $1080 °$ ，那么这个多边形的边数n＝．

查看试题解析
11. 不等式组 ${\begin{array}{l} 1 - 2 x < 3 \\ \frac{x + 1}{2} \leq 2 \end{array}$ 的所有整数解的积是．

查看试题解析
12. 如图，在 $▱ A B C D$ 中，对角线AC，BD相交于点O，过点O作OE⊥AC交AD于E，如果AE＝4，DE＝3，DC＝5，则AC长为．

查看试题解析
13. 如图，在等腰直角 $Δ A B C$ 中， $∠ A C B = 9 0^{°}$ ， $B C = 2$ ， D是AB上一个动点，以DC为斜边作等腰直角 $Δ D C E$ ，使点E和A位于CD两侧．点D从点A到点B的运动过程中， $Δ D C E$ 周长的最小值是.

查看试题解析

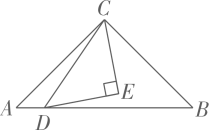
三、解答题

14. 因式分解 $x^{3} - 8 x^{2} + 16 x$ ；

查看试题解析
15. 先化简 $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，然后从 $- 1 \leq x \leq 2$ 的范围内选一个你喜欢的整数作为 $x$ 的值代入求值.

查看试题解析
16. 解方程： $\frac{x}{2 x - 3} + \frac{5}{3 - 2 x} = 4$

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ，在 $A C$ 上求作一点P，使 $P A = P B$ .（保留作图痕迹，不要求写作法和证明.）

查看试题解析
18. 已知 $(k + 3) x^{| k | - 2} + 5 < k - 4$ 是关于x的一元一次不等式，求k的值以及不等式的解集．

查看试题解析
19. 如图，点B，C分别在 $∠ A$ 的两边上，点D是 $∠ A$ 内一点， $DE ⊥ AB$ ， $DF ⊥ AC$ ，垂足分别为E，F，且 $AB = AC$ ， $DE = DF .$ 求证： $BD = CD$ ．

查看试题解析
20. 如图， $▱ A B C D$ 的对角线AC、BD相交于点O，若AC＝10cm，BD＝30cm，CD＝15cm，求 $△ A O B$ 的周长．

查看试题解析
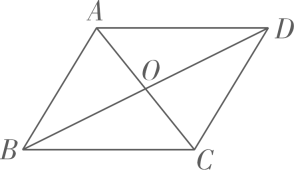21. 已知a、b、c是 $△ A B C$ 的三边，且满足 $a^{4} + b^{2} c^{2} = b^{4} + a^{2} c^{2}$ ，试判断 $△ A B C$ 的形状．阅读下面解题过程：
解：由 $a^{4} + b^{2} c^{2} = b^{4} + a^{2} c^{2}$ 得：
$a^{4} - b^{4} = a^{2} c^{2} - b^{2} c^{2}$ ①
$(a^{2} + b^{2}) (a^{2} - b^{2}) = c^{2} (a^{2} - b^{2})$ ②
即 $a^{2} + b^{2} = c^{2}$ ③
∴ $△ A B C$ 为 $R t △$ ④

(1)、试问：以上解题过程是否正确：

(2)、若不正确，请指出错在哪一步？（填代号）

(3)、本题的结论应为．

查看试题解析
22. 通州区运河两岸的“运河绿道”和步行道是健身的主要场地之一.杨师傅分别体验了60公里的“运河绿道”骑行和16公里的健步走，已知骑行的平均速度是健步走平均速度的4倍，结果健步走比骑行多用了12分钟，求杨师傅健步走的平均速度是每小时多少公里？

查看试题解析
23. 如图，直角坐标系中， $△ A B C$ 的顶点都在网格点上，其中， $C$ 点坐标为 $(1 ， 2)$ ．

(1)、填空，点A的坐标是，点B的坐标是．

(2)、将 $△ A B C$ 先向左平移2个单位长度，再向上平移1个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ，请画出 $△ A^{'} B^{'} C^{'}$ 并写出点 $C^{'}$ 的坐标为 ▲ ．

(3)、求 $△ A B C$ 的面积．

查看试题解析
24. 已知：如图，在 $▱ A B C D$ 中，点E，F在 $A C$ 上，且 $A E = C F$ .

(1)、求证：四边形 $B E D F$ 是平行四边形.

(2)、当 $A B = 3$ ， $A C = 4$ ， $A D = 5$ 时，求平行四边形 $A B C D$ 的面积.

查看试题解析
25. 某公司计划购买A，B两种型号的机器人搬运材料．已知A型机器人比B型机器人每小时多搬运30kg材料，且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同．

(1)、求A，B两种型号的机器人每小时分别搬运多少材料；

(2)、该公司计划采购A，B两种型号的机器人共20台，要求每小时搬运材料不得少于2800kg，则至少购进A型机器人多少台？

查看试题解析
26. 如图（1），在四边形 $A B C D$ 中， $A D ∥ B C$ ， $A D = 8 c m$ ， $B C = 12 c m$ ，有动点 $P$ 从 $A$ 点出发，在线段 $A D$ 上以 $1 c m / s$ 的速度向点 $D$ 运动，有动点 $Q$ 同时从 $C$ 点出发，在线段 $C B$ 上以 $2 c m / s$ 的速度向点 $B$ 运动，当其中一点到达时，另一点也随之停止运动．连接 $P Q$ ，若运动时间是 $t$ 秒．

(1)、四边形 $A B Q P$ 是平行四边形时，则 $t =$ ；

(2)、如图（2），取 $A B$ 中点 $E$ ， $C D$ 中点 $F$ ，连接 $P E$ ， $Q F$ ，请求出 $P E ∥ Q F$ 的时间 $t$ ；

(3)、在（2）中，继续连接 $E F$ ，与 $P Q$ 相交与点 $O$ ，如图（3）当 $P E ∥ Q F$ 时，请写出一个与 $E F$ 有关的结论，并证明这个结论．

查看试题解析