陕西省汉中市洋县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、3. 如图,是某水塘边的一块警示牌,牌面是正五边形,这个正五边形的每个内角为( )
2. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、3. 如图,是某水塘边的一块警示牌,牌面是正五边形,这个正五边形的每个内角为( ) A、 B、 C、 D、4. 下列各式中,不能分解因式的是( )A、 B、 C、 D、5. 下列条件中,不能判定四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( )
A、 B、 C、 D、4. 下列各式中,不能分解因式的是( )A、 B、 C、 D、5. 下列条件中,不能判定四边形是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( ) A、65° B、80° C、100° D、70°7. 若关于x的分式方程有无解,则m的值为( )A、 B、2 C、 D、48.
A、65° B、80° C、100° D、70°7. 若关于x的分式方程有无解,则m的值为( )A、 B、2 C、 D、48.如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
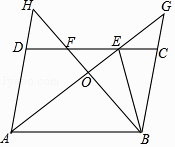 A、BO=OH B、DF=CE C、DH=CG D、AB=AE
A、BO=OH B、DF=CE C、DH=CG D、AB=AE二、填空题
-
9. 关于x的不等式的解集是.10. 如图,直线分别交坐标轴于 , 两点,则关于x的不等式的解集是 .
 11. 如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形 , 则四边形的周长是cm.
11. 如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形 , 则四边形的周长是cm.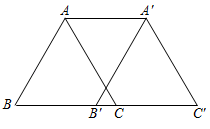 12. 如图,在中, , , , , 分别为 , , 的中点,若 , 则的长度为 .
12. 如图,在中, , , , , 分别为 , , 的中点,若 , 则的长度为 . 13. 为深入践行“绿水青山就是金山银山”的发展理念,我国绿色发展成就显著,在今年的植树造林活动期间,某苗圃公司第一天卖出一批小叶榄仁树苗共收款8000元,第二天又卖出同样的树苗收款17000元,所卖数量是第一天的2倍,售价比第一天每棵多了5元,第二天每棵树苗售价是元.
13. 为深入践行“绿水青山就是金山银山”的发展理念,我国绿色发展成就显著,在今年的植树造林活动期间,某苗圃公司第一天卖出一批小叶榄仁树苗共收款8000元,第二天又卖出同样的树苗收款17000元,所卖数量是第一天的2倍,售价比第一天每棵多了5元,第二天每棵树苗售价是元.三、解答题
-
14. 因式分解: .15. 解方程:16. 尺规作图.已知:线段 , , 求作等腰三角形 , 使其底边长为c,底角为.(不写作图作图过程,保留作图痕迹)
 17. 如图,在中,点M、N分别是对角线上的两点,且 , 连接 . 求证: .
17. 如图,在中,点M、N分别是对角线上的两点,且 , 连接 . 求证: . 18. 如图,与相交于点O , , , , 连接 , 求证;垂直平分 .
18. 如图,与相交于点O , , , , 连接 , 求证;垂直平分 . 19. 解不等式组 , 并在数轴上表示它的解集.20. 先化简,再求值: , 其中 .21. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .
19. 解不等式组 , 并在数轴上表示它的解集.20. 先化简,再求值: , 其中 .21. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .
⑴画出关于原点O的中心对称图形;
⑵画出将绕原点O顺时针旋转得到的 .
22. 八年级利用暑假组织学生外出旅游,有名家长代表随团出行,甲旅行社说:“如果名家长代表都买全票,则其余学生可享受半价优惠”;乙旅行社说:“包括名家长代表在内,全部按票价的折(即按全票的收费)优惠”,若全票价为元.请你通过计算说明:旅游人数在什么范围时选择甲旅行社费用较少?23. 如图,在中,对角线 , 相交于点O , 点E , F在上,点G , H在上,且 , .
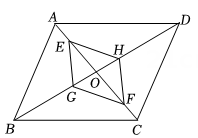 (1)、若 , , 试求的度数.(2)、求证:四边形是平行四边形.24. “以形释数”是利用数形结合思想证明代数问题的一种体现.
(1)、若 , , 试求的度数.(2)、求证:四边形是平行四边形.24. “以形释数”是利用数形结合思想证明代数问题的一种体现. (1)、如图1所示,边长为的正方形中有一个边长为的小正方形.如图2所示是由图1中的阴影部分拼成的一个长方形.请直接用含 , 的代数式表示图1中阴影部分的面积 , 图2中阴影部分的面积;(2)、写出利用图1和图2的面积关系所揭示的因式分解的公式:;(3)、如图3,将一张长方形纸板按图中实线裁剪成12块,其中有两块是边长都为的大正方形,3块是边长都为的小正方形,7块是长为 , 宽为的全等小长方形,且 . 观察图形,可以发现代数式可以因式分解两个二项一次式的乘积,那么这两个二项一次式分别是什么?25. 在中, , 点D为线段BC上一个动点(不与B、C重合),以为一边向的左侧作 , 使 , , 过点E作的平行线,交直线于点F , 连接 .
(1)、如图1所示,边长为的正方形中有一个边长为的小正方形.如图2所示是由图1中的阴影部分拼成的一个长方形.请直接用含 , 的代数式表示图1中阴影部分的面积 , 图2中阴影部分的面积;(2)、写出利用图1和图2的面积关系所揭示的因式分解的公式:;(3)、如图3,将一张长方形纸板按图中实线裁剪成12块,其中有两块是边长都为的大正方形,3块是边长都为的小正方形,7块是长为 , 宽为的全等小长方形,且 . 观察图形,可以发现代数式可以因式分解两个二项一次式的乘积,那么这两个二项一次式分别是什么?25. 在中, , 点D为线段BC上一个动点(不与B、C重合),以为一边向的左侧作 , 使 , , 过点E作的平行线,交直线于点F , 连接 . (1)、如图1,若 , 判断的形状并说明理由;(2)、若 , 如图2,判断的形状,并说明理由.26. 某实验基地的杂交水稻的亩产量是普通水稻的亩产量的2倍,现有两块试验田,A块种植杂交水稻,B块种植普通水稻,A块试验田比B块试验田少4亩.(1)、A块试验田收获水稻9600千克、B块试验田收获水稻7200千克,求普通水稻和杂交水稻的亩产量各是多少千克?(2)、为了增加产量,明年计划将种植普通水稻的B块试验田的一部分改种杂交水稻,使总产量不低于17700千克,那么至少把多少亩B块试验田改种杂交水稻?
(1)、如图1,若 , 判断的形状并说明理由;(2)、若 , 如图2,判断的形状,并说明理由.26. 某实验基地的杂交水稻的亩产量是普通水稻的亩产量的2倍,现有两块试验田,A块种植杂交水稻,B块种植普通水稻,A块试验田比B块试验田少4亩.(1)、A块试验田收获水稻9600千克、B块试验田收获水稻7200千克,求普通水稻和杂交水稻的亩产量各是多少千克?(2)、为了增加产量,明年计划将种植普通水稻的B块试验田的一部分改种杂交水稻,使总产量不低于17700千克,那么至少把多少亩B块试验田改种杂交水稻?