陕西省渭南市潼关县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 计算的结果为( )A、 B、11 C、 D、1212. 如果函数的图象经过第一、三、四象限,那么的取值范围是( )A、 B、 C、 D、3. 某位同学四次射击测试成绩(单位:环)分别为:9,9, , 8,若这组数据的众数与平均数恰好相等,则x的值为( )A、10 B、9 C、8 D、74. 如图,直线上有三个正方形 , , , 若 , 的面积分别为和 , 则的面积为( )
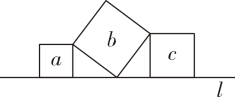 A、 B、 C、 D、5. 若点A(3,-5)和点B(-6,a)都在正比例函数y=kx的图象上,则a的值为( )A、-10 B、10 C、5 D、-36. 在四边形中, , 若四边形是平行四边形,则还需要满足( )A、 B、 C、 D、7. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )
A、 B、 C、 D、5. 若点A(3,-5)和点B(-6,a)都在正比例函数y=kx的图象上,则a的值为( )A、-10 B、10 C、5 D、-36. 在四边形中, , 若四边形是平行四边形,则还需要满足( )A、 B、 C、 D、7. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )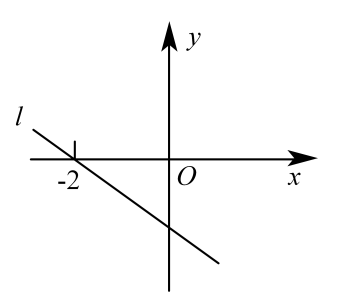 A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、8. 如图,在矩形中,E是边上一点,F , G分别是 , 的中点,连接 , , , 若 , , , 则矩形的面积是( )
A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、8. 如图,在矩形中,E是边上一点,F , G分别是 , 的中点,连接 , , , 若 , , , 则矩形的面积是( )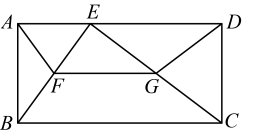 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
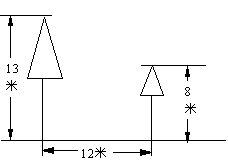
9. 若二次根式在实数范围内有意义,则的取值范围是 .10. 一组数据:6,5,7,6,6的中位数是.11. 将一次函数的图象向下平移2个单位长度后经过点 , 则b的值为 .12. 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞米.
 13. 如图,菱形的周长为20,面积为24,是对角线上一点,分别作点到直线、的垂线段、 , 则等于.
13. 如图,菱形的周长为20,面积为24,是对角线上一点,分别作点到直线、的垂线段、 , 则等于.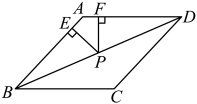
三、解答题
-
14. 计算: .15. 已知一次函数 .(1)、求m的取值范围;(2)、若这个函数的图象经过原点,求m的值.16. 如图,从电线杆离地面的点处向地面拉一条长的钢索, , 这条钢索在地面的固定点到电线杆底部点的距离是多少?
 17. 若矩形的长为 , 宽为 , 求矩形的周长和面积.18. 某电视台要招聘1名记者,某应聘者参加了3项素质测试,成绩如下:
17. 若矩形的长为 , 宽为 , 求矩形的周长和面积.18. 某电视台要招聘1名记者,某应聘者参加了3项素质测试,成绩如下:测试项目
采访写作
计算机操作
创意设计
测试成绩(分)
90
85
80
如果将采访写作、计筑机操作和创意设计的成绩按计算,则该应聘者的素质测试平均成绩是多少分?
19. 如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连接DE,CF.求证:四边形CEDF是平行四边形.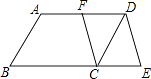 20. 如图,和以为边的正方形 , 已知 , , , 求正方形的面积.
20. 如图,和以为边的正方形 , 已知 , , , 求正方形的面积.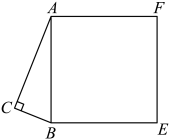 21. 在平面直角坐标系中,一次函数的图象经过点 , .(1)、求这个一次函数的解析式;(2)、若这个一次函数的图象与x轴的交点为C , 求的面积.22. 如图,在中, , , 的垂直平分线交于点 , 交于点 , 且 . 延长交的延长线于点 , 连接 .
21. 在平面直角坐标系中,一次函数的图象经过点 , .(1)、求这个一次函数的解析式;(2)、若这个一次函数的图象与x轴的交点为C , 求的面积.22. 如图,在中, , , 的垂直平分线交于点 , 交于点 , 且 . 延长交的延长线于点 , 连接 .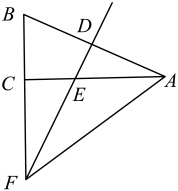 (1)、求证:;(2)、求的长.23. 已知,如图,四边形ABCD的对角线AC⊥BD于点E , 点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF , ∠CBF=∠DCB . 求证:四边形DBFC是菱形.
(1)、求证:;(2)、求的长.23. 已知,如图,四边形ABCD的对角线AC⊥BD于点E , 点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF , ∠CBF=∠DCB . 求证:四边形DBFC是菱形.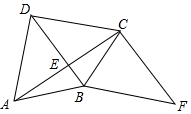 24. 为庆祝2023年两会胜利召开、学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取“整十”的计分方式,满分100分.竞赛成绩如图所示:
24. 为庆祝2023年两会胜利召开、学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取“整十”的计分方式,满分100分.竞赛成绩如图所示: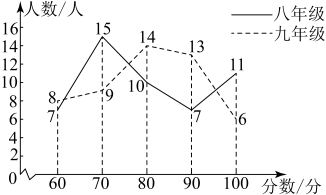
众数
中位数
方差
八年级竞赛成绩
70
80
188
九年级竞赛成绩
80
(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗?通过计算说明理由;(2)、请根据图表中的信息,回答下列问题:①表中 ▲ , ▲ ;
②现要给成绩突出的年级颁奖,结合众数和方差两个角度来分析,你认为应该给哪个年级颁奖?请说明理由.
25. A、B两个码头之间航程为48千米,甲、乙两轮船同时出发,甲轮船从A码头顺流匀速航行到B码头后,立即逆流匀速航行返回到A码头,乙轮船从B码头逆流匀速航行到A码头后停止,两轮船在静水中速度均为20千米/时,水流速度不变.两轮船距A码头的航程y(千米)与各自的航行时间x(时)之间的函数图象如图所示.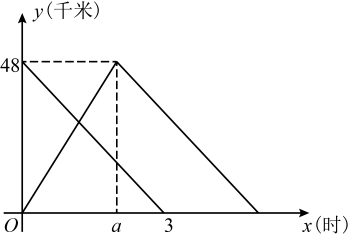
(顺流速度=静水速度+水流速度;逆流速度=静水速度-水流速度)
(1)、水流速度为千米/时;a值为;(2)、求甲轮船从B码头向A码头返回过程中y与x之间的函数关系式;(3)、当乙轮船到达A码头时,求甲轮船距A码头的航程.26. 在综合与实践活动课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动,如图1,现有矩形纸片ABCD , AB=4,BC=7.动手操作
将图1中的矩形纸片折叠,使点A落在BC边上的点F处,然后展平,得到折痕BE , 连结EF , EC , 如图2.

解决问题
请根据图2完成下列问题:
(1)、线段CF的长为 . 线段CE的长为 .(2)、试判断四边形ABFE的形状,并给予证明.(3)、拓展探究将图2中的矩形纸片再次折叠,使点D落在CE上的点N处,然后展平,得到折痕EM , 连结MN , 如图3,则线段CM的长为 .