陕西省胃南市合阳县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 中国有着丰富的物种资源,其中蝴蝶就有1600种.我国于1963年发行了一套特种邮票,共收集了我国其有代表性的20种蝴蝶,这是第6枚--美丽的粉绿燕凤蝶.下图所示的蝴蝶哪个可以通过平移得到( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、3. 今年某市约有10万余名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )A、这1000名考生是总体的一个样本 B、每位考生的数学成绩是个体 C、10万余名考生是总体 D、1000名考生是样本容量4. 如图,为了加固房屋,要在屋架上加一根横梁 , 使 . 若 , 则的度数是( )
2. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、3. 今年某市约有10万余名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )A、这1000名考生是总体的一个样本 B、每位考生的数学成绩是个体 C、10万余名考生是总体 D、1000名考生是样本容量4. 如图,为了加固房屋,要在屋架上加一根横梁 , 使 . 若 , 则的度数是( ) A、30° B、60° C、120° D、150°5. 如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )
A、30° B、60° C、120° D、150°5. 如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )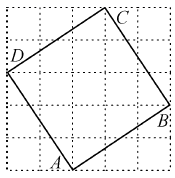 A、(2,3),(3,2) B、(3,2),(2,3) C、(2,3),(-3,2) D、(3,2),(-2,3)6. 小明在一次社会实践活动中负责了解他所居住的小区居民的家庭月人均收入情况,他从中随机调查了20户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了如下频数分布表.
A、(2,3),(3,2) B、(3,2),(2,3) C、(2,3),(-3,2) D、(3,2),(-2,3)6. 小明在一次社会实践活动中负责了解他所居住的小区居民的家庭月人均收入情况,他从中随机调查了20户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了如下频数分布表.人均收入
频数
5
9
4
2
从表中可以得出,这里组距、组数分别是( )
A、51,4 B、49,4 C、1000,4 D、1000,57. 已知方程组的解满足 , 则的值为( )A、 B、 C、2 D、48. 对于任意实数p、q,定义一种运算: , 如: , 请根据以上定义解决问题:若关于x的不等式组 有2个整数解,则m的取值范围为是( )A、3≤m<5 B、3<m≤5 C、3≤m≤5 D、3<m<5二、填空题
-
9. 一箭星新纪录!年月日,我国在太原卫星发射中心使用长征二号丁运载火箭,成功发射吉林一号高分星等颗卫星.发射前,为了确保万无一失,工程师对运载火箭的所有零部件进行了检查,调查方式应为调查.(填“全面”或“抽样”)10. 四个数-1,0, , 中,为无理数的是 .11. 《九章算术》中记载:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶田各几何?”其大意是:今有好田1亩,价值钱;坏田7亩,价值钱.今共买好、坏田1顷(1顷=亩),价钱钱.问好、坏田各买了多少亩?设好田买了x亩,坏田买了y亩,根据题意可列方程组为 .12. 当时,式子的值小于的值.13. 如图,为的边上一点,过点作 , 交的平分线于点 . 过点作 , 交的延长线于点 , 若 . 现有以下结论:①;②;③;④ . 其中正确的是 . (填序号)

三、解答题
-
14. 计算: .15. 解方程组16. 已知:点在直线l上,直线l经过 , 且与x轴平行.求P点的坐标.17. 解不等式组: , 并将解集在如图所示的数轴上表示出来.
 18.
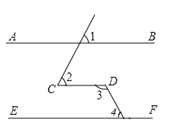
18.如图,已知∠1=∠2,∠3+∠4=180°,证明AB∥EF.
 19. 如图,在平面直角坐标系中,三角形的顶点坐标分别是 , , . 将三角形平移,使顶点B平移到坐标原点O处,得到三角形 .
19. 如图,在平面直角坐标系中,三角形的顶点坐标分别是 , , . 将三角形平移,使顶点B平移到坐标原点O处,得到三角形 . (1)、点C的对应点的坐标是;(2)、画出平移后的三角形 .20. 如图,直线和相交于点O , 把分成两部分,且 , 平分 .
(1)、点C的对应点的坐标是;(2)、画出平移后的三角形 .20. 如图,直线和相交于点O , 把分成两部分,且 , 平分 . (1)、的对顶角为 , 的邻补角为;(2)、若 , 求度数.21. 根据等式的性质和不等式的性质,我们可以得到比较两个数量大小的方法:若 , 则;若 , 则;若 , 则 , 这种比较大小的方法称为“作差比较法”,试比较与的大小.22. 已知的平方根是 , 的立方根是2,(1)、求a、b的值;(2)、求的算术平方根.23. 为参加学校的社团巡礼活动,公益社团准备用元购买水彩笔和签字笔.已知水彩笔和签字笔的单价分别为元/盒、元/盒,请问社团购买这两种笔且恰好花费元,共有哪几种购买方案?(两种都买)24. 某市为了解初中生每周锻炼身体的时长:(单位:小时)的情况,在全市随机抽取部分初中生进行调查,按五个组别:组();组();组();组();组()进行整理,绘制成如下两幅不完整的统计图.
(1)、的对顶角为 , 的邻补角为;(2)、若 , 求度数.21. 根据等式的性质和不等式的性质,我们可以得到比较两个数量大小的方法:若 , 则;若 , 则;若 , 则 , 这种比较大小的方法称为“作差比较法”,试比较与的大小.22. 已知的平方根是 , 的立方根是2,(1)、求a、b的值;(2)、求的算术平方根.23. 为参加学校的社团巡礼活动,公益社团准备用元购买水彩笔和签字笔.已知水彩笔和签字笔的单价分别为元/盒、元/盒,请问社团购买这两种笔且恰好花费元,共有哪几种购买方案?(两种都买)24. 某市为了解初中生每周锻炼身体的时长:(单位:小时)的情况,在全市随机抽取部分初中生进行调查,按五个组别:组();组();组();组();组()进行整理,绘制成如下两幅不完整的统计图.
根据图中提供的信息,解决下列问题:
(1)、求出这次抽样调查的学生总人数;(2)、补全频数分布直方图;(3)、求组所在扇形圆心角的度数.25. “粮食生产根本在耕地、出路在科技”.为提高农田耕种效率,今年开春某农村合作社计划投入资金购进甲、乙两种农耕设备,已知购进2台甲种农耕设备和1台乙种农耕设备共需4.2万元;购进1台甲种农耕设备和3台乙种农耕设备共需5.1万元.(1)、求购进1台甲种农耕设备和1台乙种农耕设备各需多少万元;(2)、若该合作社购进乙种农耕设备数比甲种农耕设备数的2倍少3台,且购进甲、乙两种农耕设备总资金不超过10万元,求最多可以购进甲种农耕设备多少台?26. 【问题背景】如图,已知直线 , 点为直线 , 之间的一个动点,连接 , , 平分 , 平分 , 和交于点 .
(1)、【问题提出】如图1,求证:;
 (2)、【拓展延伸】
(2)、【拓展延伸】如图2,连接 , 在点运动过程中,当满足 , 时:
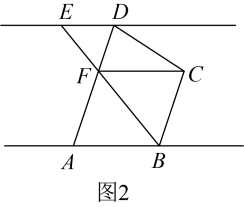
①若 , 求度数;
②若 , 求度数.