陕西省西安市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数学曲线中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列不等式成立的是（）

A、 $a - 2 < b - 2$ B、 $2 a > 2 b$ C、 $- 2 a > - 2 b$ D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
3. 要使分式 $\frac{4}{x - 3}$ 有意义，x应满足的条件是（）

A、x＞3 B、x=3 C、x＜3 D、x≠3

查看试题解析
4. 一个关于x的一元一次不等式组的解集在数轴上的表示如图，则该不等式组的解集是（）

A、x＞1 B、x≥1 C、x＞3 D、x≥3

查看试题解析
5. 下面各式从左到右的变形，属于因式分解的是（）

A、 $x^{2} - x - 1 = x (x - 1) - 1$ B、 $x^{2} - 1 = (x - 1)^{2}$ C、 $x^{2} - x - 6 = (x - 3) (x + 2)$ D、 $x (x - 1) = x^{2} - x$

查看试题解析
6. 线段MN是由线段EF经过平移得到的，若点E(﹣1，3)的对应点M(2，5)，则点F(﹣3，﹣2)的对应点N的坐标是（）

A、(﹣1，0) B、(﹣6，0) C、(0，﹣4) D、(0，0)

查看试题解析
7. 如图，在 $△ A B C$ 中， $F$ 在 $B C$ 上， $A C = C F$ ， $C D ⊥ A F$ ，垂足为 $D$ ， $E$ 为 $A B$ 的中点， $A C = 6$ ， $B C = 10$ ，则 $E D$ 的长为（）

A、4 B、3 C、 $\frac{5}{2}$ D、2

查看试题解析
8. 如图，在△ABC中，∠ABC＝60°，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且 $D E = D F = \sqrt{2}$ ，则线段BE的长为（）

A、 $\sqrt{2}$ B、 $\sqrt{6}$ C、2 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

9. 分解因式： $3 a^{2} - 21 a b =$

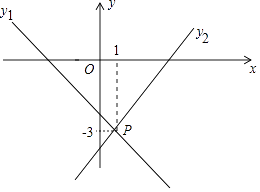
查看试题解析
10. 若一个正多边形的每一个外角都是30°，则这个正多边形的边数为．

查看试题解析
11. 如图，直线y₁=-x+a与y₂=bx-4相交于点P，已知点P的坐标为（1，-3），则关于x的不等式-x+a<bx-4的解集是.

查看试题解析
12. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(0 ， 2)$ ，点 $B$ 在 $x$ 轴上， $A B = 4$ ，将 $△ A O B$ 绕点 $B$ 顺时针旋转 $60 °$ 得到 $△ A^{'} O^{'} B$ ，则点 $A^{'}$ 的坐标为．

查看试题解析
13. 如图，已知在△ABC中，AB=AC=13，BC=10，点M是AC边上任意一点，连接MB，以MB、MC为邻边作平行四边形MCNB，连接MN，则MN的最小值是

查看试题解析

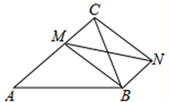
三、解答题

14. 解不等式组： ${\begin{array}{l} 2 + x > 7 - 4 x ， \\ x < \frac{4 + x}{2} . \end{array}$

查看试题解析
15. 解方程 $\frac{2}{x + 1} + 1 = \frac{x}{x - 1}$ .

查看试题解析
16. 先化简，再求值： $\frac{a}{a^{2} - 1} \cdot (a + \frac{1 - 2 a}{a})$ ，其中 $a = - 2$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A = 45 °$ ，请利用尺规作图法在AB上求作一点D ，使得 $A D = C D$ ．（保留作图痕迹，不写作法）

查看试题解析
18. 已知：如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF；求证：AD平分∠BAC．

查看试题解析
19. 如图， $△ A B C$ 是边长为 $2$ 的等边三角形，将 $△ A B C$ 沿直线 $B C$ 平移到 $△ D C E$ 的位置，连接 $B D$ ，求 $△ A B C$ 平移的距离和 $B D$ 的长．

查看试题解析
20. 某品牌护眼灯的进价为 $240$ 元，商店以 $320$ 元的价格出售．“五一”期间，商店为让利于顾客，计划以利润率不低于 $20 %$ 的价格降价出售，则该护眼灯最多可降价多少元？

查看试题解析
21. 如图，在平面直角坐标系中，一个三角板 $A B C$ 的三个顶点分别是 $A (- 3 ， 2) ， B (0 ， 4) ， C (0 ， 2)$ ．

(1)、操作与实践：
①步骤一：将三角板 $A B C$ 以点 $C$ 为旋转中心旋转 $180 °$ ，画出旋转后对应的 $△ A_{1} B_{1} C$ ；
②步骤二：平移三角板 $A B C$ ，点 $A$ 的对应点 $A_{2}$ 的坐标为 $(1 ， - 4)$ ，画出平移后对应的 $△ A_{2} B_{2} C_{2} ．$ 要求：不写作法，保留作图痕迹

(2)、应用与求解：
将 $△ A_{1} B_{1} C$ 绕某一点旋转可以得到 $△ A_{2} B_{2} C_{2}$ ，请直接写出旋转中心的坐标．

查看试题解析
22. 如图，△ABC中，∠C=90°，∠A=30°，DE垂直平分线段AC．

(1)、求证：△BCE是等边三角形．

(2)、若BC=3，求DE的长．

查看试题解析
23. 如图，在▱ $A B C D$ 中，点 $O$ 为对角线 $B D$ 的中点， $E F$ 过点 $O$ 且分别交 $A B$ 、 $D C$ 于点 $E$ 、 $F$ ，连接 $D E$ 、 $B F$ ．

(1)、求证： $△ D O F$ ≌ $△ B O E$ ；

(2)、求证： $D E = B F$ ．

查看试题解析
24. 2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势，经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元．若充电费和加油费均为200元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费．

查看试题解析
25. 近日，“盛唐密盒”爆火出圈，一举将西安再次推入文旅热门打卡城市，也带火了汉服体验 $．$ 有数据显示， $3$ 月以来，西安汉服体验订单量全国第一，比去年同期增长了 $13$ 倍 $．$ 某旅行社计划租用若干件汉服供游客体验，已知甲、乙两个汉服体验店租用单价分别是 $75$ 元 $/$ 件， $80$ 元 $/$ 件，五一期间为吸引更多顾客，甲、乙两店各自推出了不同的优惠方案，具体如下：
甲汉服体验店：按原价八折进行优惠；
乙汉服体验店：若租用不超过 $6$ 件时，按原价收取租金；若租用 $6$ 件以上，超出 $6$ 件的部分可按原价的五折进行优惠．
设该旅行社需要租用 $x (x > 6)$ 件汉服，选择甲店总租金为 $y_{1}$ 元 $．$ 选择乙店总租金为 $y_{2}$ 元．

(1)、请分别求出 $y_{1}$ ， $y_{2}$ 关于 $x$ 的函数解析式；

(2)、该旅行社选择哪家汉服体验店更便宜？

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = \frac{2}{3} x + 2$ 的图象与 $x$ 轴交于点A ，与 $y$ 轴交于点 $B$ ，且与正比例函数 $y = \frac{4}{3} x$ 的图象交点为 $C (3 ， 4) ．$ 若 $D$ 为线段 $O C$ 上的动点，过点 $D$ 作 $D E ∥ y$ 轴交 $A C$ 于点 $E ．$ 设 $D$ 点的横坐标为 $x$ ，线段 $D E$ 的长为 $y$ ．

(1)、问题提出
$y$ 与 $x$ 的函数关系式为；

(2)、若 $△ A O D$ 为等腰三角形，请求出点 $D$ 的坐标；

(3)、问题探究
平面内是否存在一点 $P$ ，使以 $O$ ， A ， $C$ ， $P$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析