陕西省西安市2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 计算的结果是( )A、 B、 C、 D、2. 如图, , 若 , 则的度数是( )
 A、 B、 C、 D、3. 2022年11月,中国矿业大学科研团队发现外径约55纳米的天然洋葱状富勒烯,即“碳洋葱”,这是目前地球上发现的最大的天然“碳洋葱”,已知1纳米米,那么55纳米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 彩民李大叔购买1张彩票,中奖这个事件是( )A、必然事件 B、确定性事件 C、不可能事件 D、随机事件5. 2022年第22届国际足联世界杯在卡塔尔举办.下列四届世界杯会徽中是轴对称图形的是( )A、
A、 B、 C、 D、3. 2022年11月,中国矿业大学科研团队发现外径约55纳米的天然洋葱状富勒烯,即“碳洋葱”,这是目前地球上发现的最大的天然“碳洋葱”,已知1纳米米,那么55纳米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 彩民李大叔购买1张彩票,中奖这个事件是( )A、必然事件 B、确定性事件 C、不可能事件 D、随机事件5. 2022年第22届国际足联世界杯在卡塔尔举办.下列四届世界杯会徽中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 我国古代把一昼夜划分成十二个时段,每一个时段叫一个时辰,古时与今时的对应关系(部分)如下表所示.天文兴趣小组的小明等4位同学从今夜23:00至明晨7:00将进行接力观测,每人两小时,观测的先后顺序随机抽签确定,小明在子时观测的概率为( )
6. 我国古代把一昼夜划分成十二个时段,每一个时段叫一个时辰,古时与今时的对应关系(部分)如下表所示.天文兴趣小组的小明等4位同学从今夜23:00至明晨7:00将进行接力观测,每人两小时,观测的先后顺序随机抽签确定,小明在子时观测的概率为( )古时
子时
丑时
寅时
卯时
今时
23:00~1:00
1:00~3:00
3:00~5:00
5:00~7:00
A、 B、 C、 D、7. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、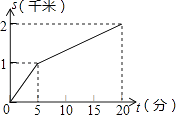 B、
B、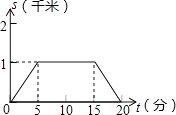 C、
C、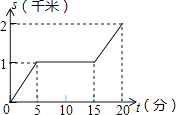 D、
D、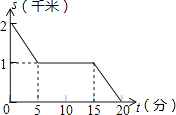 8. 如图,E是中BC边上的一点,且 , 点D是AC边中点,若 , 则( )
8. 如图,E是中BC边上的一点,且 , 点D是AC边中点,若 , 则( ) A、18 B、24 C、30 D、36
A、18 B、24 C、30 D、36二、填空题
-
9. 已知与互余,若 , 则 .10. 若m=n+2,则2m÷2n= .11. 在学校的综合实践课中,小双和小语同学利用一块边长为6cm的正方形纸板(如图①),制作了一朵芙蓉花(如图②),她们先将正方形纸板用虚线划分成36个全等的小正方形,再按其中的实线分割或七块形状不完全相同的图片并涂上不同颜色,制作成一副七巧板,最后用这副七巧板拼成了一朵芙蓉花,请问图②芙蓉花中阴影部分的面积占整朵芙蓉花面积的(不计重合部分).
 12. 在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的关系式是 .13. 如图,在等腰中, , , 是等边三角形,P是平分线上一动点连接、 , 则的最小值为 .
12. 在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的关系式是 .13. 如图,在等腰中, , , 是等边三角形,P是平分线上一动点连接、 , 则的最小值为 .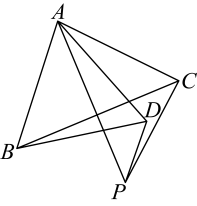
三、解答题
-
14. 计算: .15. 计算: .16. 先化简再求值: , 其中 , .17. 如图,在中, , 是的补角,请用尺规作图法,求作射线 , 使 . (保留作图痕迹,不写作法)
 18. 如图, , , , 与全等吗?请你说出理由.
18. 如图, , , , 与全等吗?请你说出理由. 19. 如图,在正方形网格中,每个小正方形的边长都是 , 每个小正方形的顶点叫做格点.网格中有一个格点(即三角形的顶点都在格点上).
19. 如图,在正方形网格中,每个小正方形的边长都是 , 每个小正方形的顶点叫做格点.网格中有一个格点(即三角形的顶点都在格点上). (1)、画出关于直线的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.20. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长.
(1)、画出关于直线的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.20. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长. 21. 完成下面推理过程:
21. 完成下面推理过程:如图,已知 , 可得// .

理由是:∵(已知),
( ).
∴( )
∴//( )
∴( ).
∵(已知),
∴∠_▲_(等量代换),
∴//( ).
22. 一个不透明的箱子里装有红、黄、蓝三种颜色的小球共30个,它们除颜色外其他均相同,其中红色球有6个、黄色球的数量是蓝色球数量的2倍.(1)、求摸出1个球是蓝色球的概率;(2)、再往箱子中放入多少个蓝色球,可以使摸出1个蓝色球的概率为?23. 如图,AC⊥BC , BD平分∠ABE , CD//AB交BD于点D , ∠1=25°,求∠2的度数. 24. 为了体验大学校园文化,小华周末骑电动车从家出发去西安交大,当他骑了一段路时,想起要帮在交大读书的张浩买一本书,于是原路返回到刚经过的书店,买到书后继续前往交大,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息解答下列问题:
24. 为了体验大学校园文化,小华周末骑电动车从家出发去西安交大,当他骑了一段路时,想起要帮在交大读书的张浩买一本书,于是原路返回到刚经过的书店,买到书后继续前往交大,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息解答下列问题: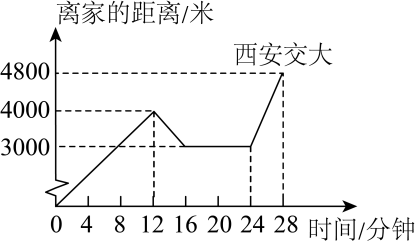 (1)、小华家离西安交大的距离是多少?书店离家多远?(2)、小华在书店停留了多长时间?(3)、本次去西安交大途中,小华一共行驶了多少米?其中小华买到书后从书店前往西安交大的速度为多少?25. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 , 请解答下列问题:
(1)、小华家离西安交大的距离是多少?书店离家多远?(2)、小华在书店停留了多长时间?(3)、本次去西安交大途中,小华一共行驶了多少米?其中小华买到书后从书店前往西安交大的速度为多少?25. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 , 请解答下列问题: (1)、写出图2中所表示的数学等式.(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:若 , , 则.26. 【知识背景】在同一平面内,两条直线的位置关系有两种,分别是平行和相交,在相交这种位罟关系中,包括垂直这种特殊位置关系.(1)、【问题探究】
(1)、写出图2中所表示的数学等式.(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:若 , , 则.26. 【知识背景】在同一平面内,两条直线的位置关系有两种,分别是平行和相交,在相交这种位罟关系中,包括垂直这种特殊位置关系.(1)、【问题探究】如图1, , , 分别在 , 上,平分交于点C , D是直线上一点,平分交于点E .
①若D在点B的右侧,且 , , 求的度数为 ▲ .

②如图2,当D在点B的右侧时,过点E作 , 垂足为 , 记 , , 直接写出y与x的关系式.
(2)、【拓展应用】“一带一路”让中国和世界联系更紧密,“中欧班列”为了安全起见在某段铁路两旁安置了A , B两座可旋转探照灯.如图3,假定主道路是平行的,即 , 连在 , 且 . 灯发出的射线自顺时针旋转至便立即回转,灯B发出的射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.灯A转动的速度是3度/秒,灯B转动的速度是9度/秒,若它们同时开始转动,设转动时间为t秒,在灯A发出的射线从转至的过程中,与互相垂直时,请直接写出此时t的值.
