陕西省咸阳市秦都区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 光的速度非常快,传播1米仅需要秒,将数据用科学记数法表示正确的是( )A、 B、 C、 D、2. 中华姓氏源于上古,每个姓氏都有自己的图腾.下列姓氏图腾是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片 B、中秋节晚上能看到月亮 C、买100张彩票一定会中奖 D、在只装有红球的袋中摸出1个球是红球4. 如图,点E在的延长线上,下列条件中,能判定的是( )
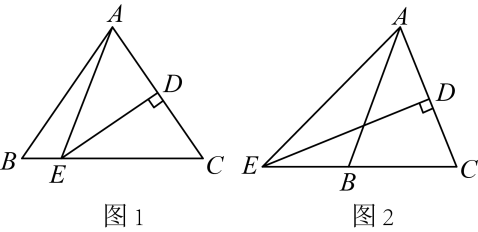
3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片 B、中秋节晚上能看到月亮 C、买100张彩票一定会中奖 D、在只装有红球的袋中摸出1个球是红球4. 如图,点E在的延长线上,下列条件中,能判定的是( )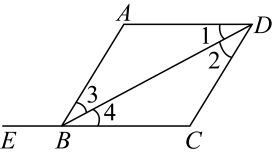 A、 B、 C、 D、5. 下列运算中,正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( )
A、 B、 C、 D、5. 下列运算中,正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( ) A、 B、 C、 D、7. 小丽从家里出发去超市购物,购物完后从超市返回家中,小丽离家的路程y(米)和所经过的时间x(分)之间的关系如图所示,则下列说法错误的是( )
A、 B、 C、 D、7. 小丽从家里出发去超市购物,购物完后从超市返回家中,小丽离家的路程y(米)和所经过的时间x(分)之间的关系如图所示,则下列说法错误的是( )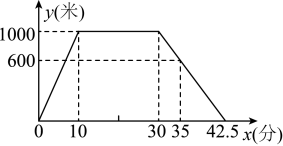 A、小丽家到超市的路程是1000米 B、小丽在超市购物用时20分钟 C、当时,小丽离家的路程是600米 D、小丽购物完从超市回到家用时分钟8. 如图,在中, , D为上的一点, , 在的右侧作 , 使得 , , 交于点O , 连接 , 若 , 则的度数为( )
A、小丽家到超市的路程是1000米 B、小丽在超市购物用时20分钟 C、当时,小丽离家的路程是600米 D、小丽购物完从超市回到家用时分钟8. 如图,在中, , D为上的一点, , 在的右侧作 , 使得 , , 交于点O , 连接 , 若 , 则的度数为( )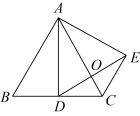 A、120° B、102° C、150° D、124°
A、120° B、102° C、150° D、124°二、填空题
-
9. 如图,已知平分 , , 当°时, .
 10. 如图,是一个材质均匀的转盘,转盘分成8个全等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止(若指针指向两个扇形的交线时,当作指向右边的扇形),转动一次转盘,转盘停止后指针指向红色扇形的概率是 .
10. 如图,是一个材质均匀的转盘,转盘分成8个全等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止(若指针指向两个扇形的交线时,当作指向右边的扇形),转动一次转盘,转盘停止后指针指向红色扇形的概率是 .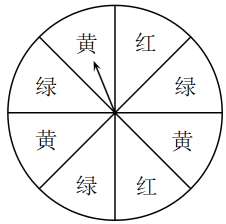 11. 如图,在中, , 平分 , 于点E , 如果 , 则的长为 .
11. 如图,在中, , 平分 , 于点E , 如果 , 则的长为 .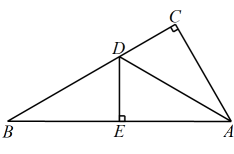 12. 某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)与1吨水的买入价x(元)的关系如表:
12. 某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)与1吨水的买入价x(元)的关系如表:1吨水的买入价x(元)
2
4
6
8
10
利润y(元)
202
200
198
196
194
当用1吨水生产的饮料所获的利润y为190元时,买入1吨水需要元.
13. 如图,在中, , 点D是内部一点, , 点E是边上一点,若平分 , , 则的度数为 .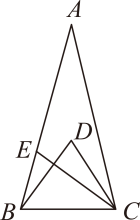
三、解答题
-
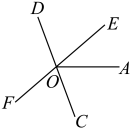
14. 计算:15. 如图,直线与交于点O,平分 , 若 , 求的度数.
 16. 某足球运动员在同一条件下进行射门,结果如表所示:
16. 某足球运动员在同一条件下进行射门,结果如表所示:射门次数n
20
50
100
200
500
800
踢进球门的频数m
13
a
58
104
255
400
踢进球门的频率
b
根据表格中的数据解答下列问题:
(1)、填空: , ;(2)、这名足球运动员在同一条件下再射门一次,估计他踢进球门的概率(结果精确到)17. 如图,已知△ABC , 利用尺规作∠ABC的平分线BD , 交AC于点D . (不写作法,保留作图痕迹)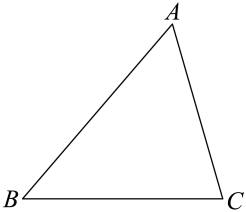 18. 小王用电脑设计图案时,先设计图案的一半,如图,然后点击对称键得到整个图案.请你在图中以直线l为对称轴,画出他设计的图案的另一半.
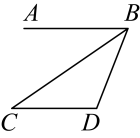
18. 小王用电脑设计图案时,先设计图案的一半,如图,然后点击对称键得到整个图案.请你在图中以直线l为对称轴,画出他设计的图案的另一半.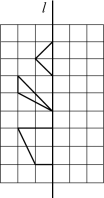 19. 如图,已知 , 和相等吗?请说明理由.
19. 如图,已知 , 和相等吗?请说明理由. 20. 先化简,再求值: , 其中 , .21. 如图,在中, , 点E、F在上,连接 , 且 . 已知 , 试证明 .
20. 先化简,再求值: , 其中 , .21. 如图,在中, , 点E、F在上,连接 , 且 . 已知 , 试证明 . 22. 桌上放有20张卡片,正面分别标有数字1到20,这些卡片除所标数字外完全相同,将背面朝上混合在一起,小乐从这20张卡片中任取一张,求下列事件发生的概率:(1)、抽到的卡片上数字比15小的概率;(2)、抽到的卡片上数字是6的倍数的概率;(3)、抽到的卡片上数字既是2的倍数,又是5的倍数的概率.23. 课间,小明拿着老师的直角三角尺玩,不小心掉到两堆砖块之间,如图所示,已知 , , , .
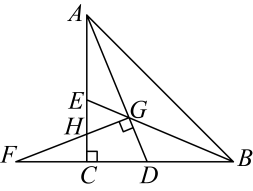
22. 桌上放有20张卡片,正面分别标有数字1到20,这些卡片除所标数字外完全相同,将背面朝上混合在一起,小乐从这20张卡片中任取一张,求下列事件发生的概率:(1)、抽到的卡片上数字比15小的概率;(2)、抽到的卡片上数字是6的倍数的概率;(3)、抽到的卡片上数字既是2的倍数,又是5的倍数的概率.23. 课间,小明拿着老师的直角三角尺玩,不小心掉到两堆砖块之间,如图所示,已知 , , , .
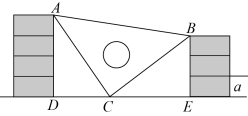 (1)、试说明:;(2)、已知 , 请你帮小明求出砖块的厚度a(每块砖的厚度相同)24. 某地粮库需要把晾晒场上的120吨小麦入库封存,受设备影响,平均每天入库15吨,入库所用的时间为x(单位:天),未入库小麦的质量为y(单位:吨)(1)、写出未入库小麦的质量y与入库所用的时间x之间的关系式;(2)、当时,未入库小麦的质量有多少吨?(3)、当x为多少时,未入库小麦的质量为45吨?
(1)、试说明:;(2)、已知 , 请你帮小明求出砖块的厚度a(每块砖的厚度相同)24. 某地粮库需要把晾晒场上的120吨小麦入库封存,受设备影响,平均每天入库15吨,入库所用的时间为x(单位:天),未入库小麦的质量为y(单位:吨)(1)、写出未入库小麦的质量y与入库所用的时间x之间的关系式;(2)、当时,未入库小麦的质量有多少吨?(3)、当x为多少时,未入库小麦的质量为45吨?