陕西省咸阳市秦都区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $a > b$ ，下列不等式的变形不正确的是（）

A、 $a - 1 > b - 1$ B、 $a - c > b - c$ C、 $2 a > 2 b$ D、 $a c > b c$

查看试题解析
3. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 90 ° ， ∠ B$ 的度数是（）

A、 $100 °$ B、 $45 °$ C、 $90 °$ D、 $135 °$

查看试题解析
4. 下列各式中能用完全平方公式因式分解的是（）

A、 $x^{2} + x$ B、 $x^{2} - 2 x y + y^{2}$ C、 $x^{2} - 1$ D、 $x^{2} - 2 x + 2$

查看试题解析
5. 如图，在 $△ A B C$ 中，点O是 $△ A B C$ 内一点，连接 $O B$ 、 $O C$ ， $O D$ 垂直平分 $A B$ ，若 $∠ O B C = ∠ O C B$ ， $O C = 4$ ，则点A、O之间的距离为（）

A、4 B、8 C、2 D、6

查看试题解析
6. 若关于x的分式方程 $\frac{3}{x - 4} + \frac{x + m}{4 - x} = 1$ 有增根，则m的值是（）

A、0 B、1 C、2 D、 $- 1$

查看试题解析
7. 如图，E是 $▱ A B C D$ 的边 $A D$ 的延长线上一点，连接 $B E$ 交 $C D$ 于点F ，连接 $C E$ ， $B D$ ．添加以下条件，仍不能判定四边形 $B C E D$ 为平行四边形的是（）

A、 $∠ A B D = ∠ D C E$ B、 $∠ A E C = ∠ C B D$ C、 $E F = B F$ D、 $A B = D B$

查看试题解析
8. 如图，在平行四边形ABCD中，分别以AB､AD为边向外作等边△ABE､△ADF ，延长CB交AE于点G ，点G在点A､E之间，连接CE､CF､EF ，则以下四个结论：①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边三角形；④CG⊥AE ．一定正确的有（）个

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

9. 若分式 $\frac{x - 1}{2 - x}$ 的值为零，则x的值为．

查看试题解析
10. 若 $a^{2} b - a b^{2} = - 6 ， a b = 3$ ，则 $a - b$ 的值为．

查看试题解析
11. 一个多边形的内角和与它的外角和之比为 $3 ： 1$ ，则这个多边形的边数是．

查看试题解析
12. 如图，已知Rt△ABC ， ∠ACB＝90°，∠B＝60°，AB＝8，将△ABC沿BC方向平移7个单位长度得到△DEF ，则图中四边形ACED的面积为．

查看试题解析
13. 如图，在 $△ A B C$ 中，点E ， F分别是AB ， AC的中点，点D是线段EF上一点，连结BD ，并延长至点G ，使得 $G D = B D$ ．连结AG ．若 $B C - A G = 1 c m$ ．则DF的长为 $c m$ ．

查看试题解析

三、解答题

14. 分解因式： $2 m^{3} n - 32 m n$ ．

查看试题解析
15. 解方程： $\frac{2 x}{x - 2} - 2 = \frac{1}{x (x - 2)}$

查看试题解析
16. 如图，在 $△ A B C$ 中，请用尺规作图法求作线段 $A D$ ，点D在边 $B C$ 上，且 $S_{A B D} ： S_{A C D}$ $= A B ： A C$ ．（不写作法，保留作图痕迹）

查看试题解析
17. 如图，在 $△ A B C$ 中， $D$ 是 $B C$ 的中点，过点 $D$ 作 $D E ∥ A C$ 交 $A B$ 于点 $E$ ，且 $D E = B E$ ，连接 $A D$ ，求证： $A D ⊥ B C$ ．

查看试题解析
18. 如图所示，在四边形ABCD中，已知AB=CD，AD=BC，DE=BF，且点E、F分别在AD、CB的延长线上．求证：BE=DF．

查看试题解析
19. 解不等式组 ${\begin{array}{l} x + 8 > 4 x - 1 \\ \frac{2}{3} x \geq - 2 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
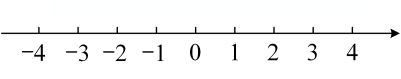20. 先化简，再求值： $(1 - \frac{m}{m + 2}) \div \frac{m^{2} - 4 m + 4}{m^{2} - 4} ，$ 其中 $m = 10$ ．

查看试题解析
21. 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，且三个顶点的坐标分别为A（-3，2）、B（0，2）、C（-1，0）．
⑴将△ABC先向上平移1个单位，再向右平移4个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点A的对应点A₁的坐标；
⑵请画出△ABC以原点O为旋转中心，逆时针旋转90°所得的△A₂B₂C₂ ．

查看试题解析
22. 如图， $△ A B C$ 是等边三角形，点E在 $A C$ 边上，连接 $B E$ ，将 $B E$ 绕点B逆时针旋转60°得到 $B D$ ，连接 $D E 、 A D$ ．

(1)、求证： $A D = C E$ ；

(2)、若 $B C = 8 c m ， B E = 7 c m$ ，求 $△ A D E$ 的周长．

查看试题解析
23. 把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．如：
①用配方法分解因式： $a ² + 4 a + 3$ ．

解：原式： $= a ² + 4 a + 4 - 1 = (a + 2) ² - 1 = (a + 2 + 1) (a + 2 - 1) = (a + 3) (a + 1)$

② $M = 2 a^{2} - 4 a + 6$ ，利用配方法求M的最小值．

解： $M = 2 a^{2} - 4 a + 6 = 2 (a^{2} - 2 a + 1) + 6 - 2 = 2 (a - 1)^{2} + 4$

$∵ 2 (a - 1)^{2} \geq 0 ， ∴ 2 (a - 1)^{2} + 4 \geq 4 ，$

∴当 $a = 1$ 时，M有最小值4．

请根据上述材料解决下列问题：

(1)、用配方法因式分解 $x ² - 4 x - 12$ ；

(2)、若 $M = 4 x^{2} + 4 x - 1$ ，求M的最小值．

查看试题解析
24. 如图，在 $△ A B C$ 中，点D是边 $B C$ 的中点，点F、G在边 $A B$ 上， $A G = A C ， A E ⊥ C G$ 交 $C G$ 于E ， $E F ∥ B C$ ．

(1)、求证：四边形 $B D E F$ 是平行四边形；

(2)、若 $A B = 10 ， A C = 6$ ，求 $B F$ 的长．

查看试题解析
25. 为了减少工人在搬运化工原料受到危害，某物流公司引进机器人，一个机器人比一个工人每小时多搬运420kg，机器人搬运900kg所用的时间与10个工人搬运600kg所用的时间相等．

(1)、求一个机器人与一个工人每小时分别搬运多少化工原料？

(2)、现在需要搬运化工原料3600kg，有3个机器人参与搬运，问至少还需要安排多少个工人才能在2个小时内搬运完？

查看试题解析
26.

(1)、阅读理解：如图①，在四边形ABCD中，AB $∥$ CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，CD之间的等量关系．
解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB＝CF，从而把AB，AD，CD转化在一个三角形中即可判断：AB，AD，CD之间的等量关系为；

(2)、问题探究：如图②，在四边形ABCD中，AB $∥$ CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论；

(3)、问题解决：如图③，AB $∥$ CF，AE与BC交于点E，且点E是BC的中点，点D在线段AE上，且∠EDF＝∠BAE＝30°，若AB＝6，CF＝2，求CD的值．

查看试题解析