江苏省徐州市睢宁县常青藤教育2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、2 B、±2 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
2. 下列四个图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点 $P (2 ， - 3)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知正比例函数y＝kx的图象经过点（-2，1），则k的值（）

A、-2 B、- $\frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
5. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{32}$ B、 $\sqrt{4 x^{2} y}$ C、 $\sqrt{\frac{x}{y}}$ D、 $\sqrt{4 x^{2} + 1}$

查看试题解析
6. 如图，若BD为等边△ABC的一条中线，延长BC至点E，使CE＝CD＝1，连接DE，则DE的长为（）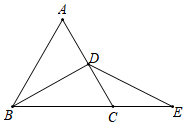

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\sqrt{5}$

查看试题解析
7. 如图，在等腰直角三角形 $A B C$ 中， $∠ B A C ＝ 90 °$ ，一个三角尺的直角顶点与 $B C$ 边的中点 $O$ 重合，且两条直角边分别经过点 $A$ 和点 $B$ ，将三角尺绕点 $O$ 按顺时针方向旋转任意一个锐角，当三角尺的两直角边与 $A B$ ， $A C$ 分别交于点 $E$ ， $F$ 时，下列结论中错误的是（）

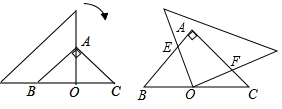A、 $A E ＋ A F = A C$ B、 $∠ B E O ＋ ∠ O F C = 180 °$ C、 $O E + O F = \frac{\sqrt{2}}{2} B C$ D、 $S_{四边形 A E O F} = \frac{1}{2} S_{Δ A B C}$

查看试题解析
8. 如图所示，四边形 $O A B C$ 是正方形，边长为4，点A、C分别在x轴、y轴的正半轴上，点P在 $O A$ 上，且P点的坐标为 $(3 ， 0)$ ， Q是 $O B$ 上一动点，则 $P Q + A Q$ 的最小值为（）

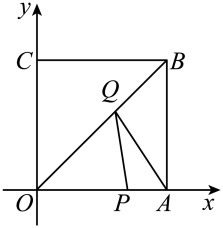A、3 B、4 C、5 D、6

查看试题解析

二、填空题

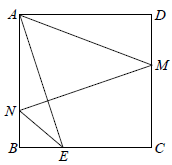
9. 如图，E为正方形ABCD中BC边上的一点，且AB=3BE=6，M、N分别为边CD、AB上的动点，且始终保持MN⊥AE，则AM+NE的最小值为．

查看试题解析
10. 已知实数 $a$ 、 $b$ 满足 $\sqrt{a - 3} + | 6 - b | = 0$ ，则 $\frac{b}{\sqrt{a}}$ 的值为．

查看试题解析
11. 化简 $\frac{4 a}{a^{2} - 4} - \frac{a}{a - 2}$ 的结果是

查看试题解析
12. 如图，在△ABC中，∠C＝90°，∠B＝22.5°，DE垂直平分AB交BC于点E，EC＝2，则△ACE的面积为．

查看试题解析
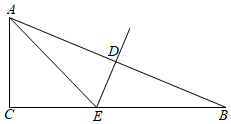13. 如图，直线y₁=-x+a与y₂=bx-4相交于点P，已知点P的坐标为（1，-3），则关于x的不等式-x+a<bx-4的解集是.

查看试题解析
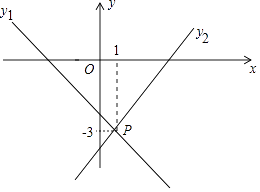14. 已知关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有实数根，则k的取值范围是.

查看试题解析
15. 如图，在直角坐标系中，点 $A ， B$ 的坐标分别为 $（ 2 ， 4 ）$ 和 $（ 3 ， 0 ）$ ，点 $C$ 是 $y$ 轴上的一个动点，且 $A 、 B 、 C$ 三点不在同一条直线上，在运动的过程中，当 $△ A B C$ 是以 $A B$ 为底的等腰三角形时，点 $C$ 的纵坐标为．

查看试题解析
16. 已知： $a^{2} + b^{2} = 3 a b (a > b > 0)$ ，则 $\frac{a + b}{a - b}$ 的值为

查看试题解析

三、解答题

17.

(1)、 $4 \sqrt{6} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{6} + \sqrt{12} .$

(2)、先化简再求值 $(\frac{a^{2} - 4}{a^{2} - 4 a + 4} - \frac{1}{a - 2}) \div \frac{a + 1}{a + 2}$ ，其中 $a = 3$

查看试题解析
18. 如图，已知过点 $B (1 ， 0)$ 的直线 $l_{1}$ 与直线 $l_{2}$ ： $y = 2 x + 4$ 相交于点 $P (- 1 ， a)$ .

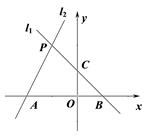(1)、求直线 $l_{1}$ 的解析式；

(2)、求四边形 $P A O C$ 的面积.

查看试题解析
19. 如图，已知∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．

(1)、求证：△AEC≌△BED；

(2)、若∠1＝44°，求∠BDE的度数．

查看试题解析
20. 为了节能减排，我区某校准备购买某种品牌的节能灯，已知4只A型节能灯和5只B型节能灯共需55元，2只A型节能灯和1只B型节能灯共需17元.

(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元？

(2)、学校准备购买这两种型号的节能灯共300只，要求A型节能灯的数量不超过B型节能灯的数量的2倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析

四、填空题

21. 将边长为2的正方形OABC如图放置，O为原点．若∠α=15°，则点B的坐标为．

查看试题解析
22. 已知正比例函数 $y_{1} = k_{1} x (k_{1} \neq 0)$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图像有一个交点的坐标为 $(3 ， - 1)$ ，则关于 $x$ 的不等式 $k_{1} x - \frac{k_{2}}{x} > 0$ 的解集为．

查看试题解析

五、解答题

23. 如图1，在平面直角坐标系中，四边形 $O A B C$ 的顶点 $A$ 、 $C$ 分别在 $x$ 、 $y$ 轴的正半轴上，点 $A$ 的坐标为 $(8 ， 0)$ ， $A B ∥ O C$ ，直线 $y = - \frac{1}{3} x + 6$ 经过点 $B$ 、 $C$ ．

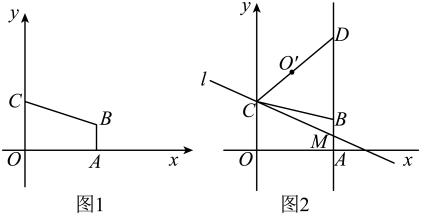(1)、点C的坐标为（），点B的坐标为（）；

(2)、设点P是x轴上的一个动点，若以点P、A、C为顶点的三角形是等腰三角形，求点P的坐标．

(3)、如图2，直线 $l$ 经过点 $C$ ，与直线 $A B$ 交于点 $M$ ，点 $O$ 关于直线 $l$ 的对称点 $O^{'}$ ，连接并延长 $C O^{'}$ ，交直线 $A B$ 于第一象限的点 $D$ ．当 $C D = 10$ 时，求直线 $l$ 的解析式．

查看试题解析
24. 如图，在平面直角坐标系中， $B$ 、 $C$ 两点在轴的正半轴上，以线段 $B C$ 为边向上作正方形 $A B C D$ ，顶点 $A$ 在正比例函数 $y = 2 x$ 的图像上，反比例函数 $t = \frac{k}{x} (x > 0 ， k > 0)$ 的图像经过点 $A$ ，且与边 $C D$ 相交于点 $E$ ．

(1)、若 $B C = 4$ ，求点 $E$ 的坐标；

(2)、连接 $A E$ ， $O E$ ．
①若 $△ A O E$ 的面积为24，求 $k$ 的值；

②是否存在某一位置使得 $A E ⊥ O A$ ，若存在，求出 $k$ 的值；若不存在，请说明理由．

查看试题解析