江苏省扬州市高邮市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-23 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、直角梯形 C、平行四边形 D、矩形2. 下列说法正确的是( )A、“打开电视,播放广告”是必然事件 B、为了了解全市中学生的视力情况,选择普查 C、过十字路口,遇到绿灯是随机事件 D、若抽奖的中奖概率为 , 则抽奖2次就能中奖3. 我们经常将调查、收集得来的数据用各类统计图进行整理与表示,下列统计图中,能反映样本或总体的分布情况的是( )A、条形图 B、扇形图 C、折线图 D、频数分布直方图4. 下列二次根式中,能与合并的是( )A、 B、 C、 D、5. 若方程没有实数根,则的值可以是( )A、 B、 C、 D、6. 如图,在中,D,E,F分别是 , 和边的中点,若添加一个条件,使四边形为矩形,则下列添加的条件可以是( )
 A、 B、 C、 D、7. 若点 , 在反比例函数的图像上,则m满足( )A、 B、 C、 D、或8. 如图,中, , , 点O是的中点,将直角三角板的直角顶点绕点O旋转,三角板的两条直角边分别与、分别交于点M、N(不与端点重合),连接 , 设三角板与重叠部分的四边形的面积为S,则下列说法正确的是( )
A、 B、 C、 D、7. 若点 , 在反比例函数的图像上,则m满足( )A、 B、 C、 D、或8. 如图,中, , , 点O是的中点,将直角三角板的直角顶点绕点O旋转,三角板的两条直角边分别与、分别交于点M、N(不与端点重合),连接 , 设三角板与重叠部分的四边形的面积为S,则下列说法正确的是( ) A、S变化,有最大值 B、S变化,有最小值 C、S不变,有最大值 D、S不变,有最小值
A、S变化,有最大值 B、S变化,有最小值 C、S不变,有最大值 D、S不变,有最小值二、填空题
-
9. 若分式在实数范围内有意义,则 x的取值范围是 .10. 某校为了有效落实“双减”政策,切实减轻学生过重的作业负担,针对八年级500名学生每天做课后作业的总时间情况进行调查,从中随机抽取了50名学生进行每天做课后作业的总时间情况的调查,该调查中的样本容量是 .11. 为执行国家药品降价政策,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程为 .12. 在质地均匀的小立方体中,有一个面上标有数字1,有两个面上标有数字2,有三个面上标有数字3,抛掷这个小立方体,则向上一面的数字可能性最大的是 .13. 若反比例函数y=的图像经过第二、四象限,则m的取值范围是 .14. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E,若 , 则的长是 .
 15. 关于x的分式方程有增根,则m的值是 .16. 若 , 则的值为 .17. 如图,已知点A在反比例函数的图像上,连接交反比例函数的图像于点B,分别过A、B两点分别作轴于点D、轴于点C,若直角梯形的面积为5,则 .
15. 关于x的分式方程有增根,则m的值是 .16. 若 , 则的值为 .17. 如图,已知点A在反比例函数的图像上,连接交反比例函数的图像于点B,分别过A、B两点分别作轴于点D、轴于点C,若直角梯形的面积为5,则 . 18. 如图,在平面直角坐标系中,点P是y轴正半轴上的一个动点,点A在x轴的正半轴上, , 将点P绕点A顺时针旋转至点 , 点M是线段的中点,若点Q是x轴的正半轴上的一个动点 , 且点N是的中点,则线段长的最小值为 .
18. 如图,在平面直角坐标系中,点P是y轴正半轴上的一个动点,点A在x轴的正半轴上, , 将点P绕点A顺时针旋转至点 , 点M是线段的中点,若点Q是x轴的正半轴上的一个动点 , 且点N是的中点,则线段长的最小值为 .
三、解答题
-
19. 计算:(1)、;(2)、 .20. 先化简,再求值: , 其中 .21. 国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出,要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法,抽取了八年级部分学生,对他们一周内平均每天的睡眠时间t(单位:h)进行了调查,将数据整理后得到下列不完整的统计图表:

学生睡眠时间频数分布表
组别
睡眠时间分组
频数
频率
A
4
B
8
C
10
a
D
21
E
b
请根据图表信息回答下列问题:
(1)、频数分布表中, , ;(2)、扇形统计图中,C组所在扇形的圆心角的度数是;(3)、请估算该校800名八年级学生中睡眠不足7小时的人数.22. 为某批篮球的质量检验结果如下:抽取的篮球数n
100
200
400
600
800
1000
1200
优等品的频数m
93
192
380
561
b
941
1128
优等品的频率m/n
a
(1)、此次调查方式为(填“普查”或“抽样调查”);(2)、补全表中数据: , ;(3)、从这批篮球中,任意抽取的一只篮球是优等品的概率的估计值为(精确到).23. 在“慈善一日捐”活动中,甲、乙两校教师各捐款30000元,若甲校教师比乙校教师人均多捐50元,给出如下三个信息:①乙校教师的人数比甲校的教师人数多;
②甲、乙两校教师人数之比为5:6;
③甲校比乙校教师人均捐款多;
请从以上三个信息中选择一个作为条件,求甲、乙两校教师的人数各有多少人?
你选择的条件是 ▲ (填序号),并根据你选择的条件给出求解过程.
24. 在菱形中,对角线相交于点O点E为的中点,连接 , 分别过点E、O作的垂线,垂足为F、G. (1)、求证:四边形为矩形;(2)、若 , , 求的面积.25. 如图,在矩形中 .
(1)、求证:四边形为矩形;(2)、若 , , 求的面积.25. 如图,在矩形中 . (1)、仅用直尺和圆规在矩形的边上找一点E,使平分 . (不写作法,保留作图痕迹)(2)、在(1)的条件下, , , 求的长.26. 已知关于x的一元二次方程 .(1)、求证:无论m取何值,方程都有两个不相等的实数根;(2)、如果方程的两个实数根为 , , 且为整数,求整数m所有可能的值.27. 如图,点P是y轴正半轴上的一个动点,过点P作y轴的垂线,与反比例函数的图象交于点A.把直线l上方的反比例函数图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“的l镜像”.
(1)、仅用直尺和圆规在矩形的边上找一点E,使平分 . (不写作法,保留作图痕迹)(2)、在(1)的条件下, , , 求的长.26. 已知关于x的一元二次方程 .(1)、求证:无论m取何值,方程都有两个不相等的实数根;(2)、如果方程的两个实数根为 , , 且为整数,求整数m所有可能的值.27. 如图,点P是y轴正半轴上的一个动点,过点P作y轴的垂线,与反比例函数的图象交于点A.把直线l上方的反比例函数图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“的l镜像”.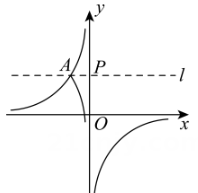 (1)、当时;
(1)、当时;①点“的l镜像”;(填“在”或“不在”)
②“的l镜像”与x轴交点坐标是;
(2)、过y轴上的点作y轴垂线,与“的l镜像”交于点B、C,若 , 求的长.28. 在正方形中, , E、F分别是、边上的动点,以、为边作平行四边形 . (1)、如图1,连接 , 交于点O,若 .
(1)、如图1,连接 , 交于点O,若 .①试说明与的关系;
②线段最小值是 ▲ ;
(2)、如图2,若四边形为菱形,判断线段与之间的数量关系,并说明理由.