江苏省扬州市广陵区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 我国新能源汽车发展迅猛，下列新能源汽车标志既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查适合用普查方式的是（）

A、某品牌灯泡的使用寿命 B、全班学生最喜爱的体育运动项目 C、长江中现有鱼的种类 D、全市学生的家庭1周内丢弃塑料袋的数量

查看试题解析
3. 在下列式子中， $x$ 可以取2和3的是（）

A、 $\sqrt{x - 2}$ B、 $\sqrt{x - 3}$ C、 $\frac{1}{x - 2}$ D、 $\frac{1}{x - 3}$

查看试题解析
4. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{15}$ B、 $\sqrt{18}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{9}$

查看试题解析
5. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $\frac{2}{2 + x}$ B、 $- \frac{2}{2 + x}$ C、 $\frac{2}{x - 2}$ D、 $- \frac{2}{x - 2}$

查看试题解析
6. 如图，在 $△ A B C$ 中，点D，E分别是 $A C ， B C$ 的中点，以点A为圆心， $A D$ 为半径作圆弧交 $A B$ 于点F.若 $A D = 7$ ， $D E = 5$ ，则 $B F$ 的长为（）

A、2 B、2.5 C、3 D、3.5

查看试题解析

7. 做随机抛掷一枚纪念币的试验，得到的结果如下所示：

抛掷次数m	500	1000	1500	2000	2500	3000	4000	5000
“正面向上的次数n”	265	512	793	1034	1306	1558	2083	2598
“正面向上的频率 $\frac{n}{m}$ ”	0.530	0.512	0.529	0.517	0.522	0.519	0.521	0.520

下面有 3 个推断：

①当抛掷次数是 1000 时， “正面向上”的频率是 0.512，所以“正面向上”的概率是0.512；
②随着试验次数的增加， “正面向上”的频率总在 0.520 附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是 0.520；
③若再次做随机抛掷该纪念币的实验，则当抛掷次数为 3000 时，出现“正面向上”的次数不一定是 1558 次．

其中所有合理推断的序号是（）

A、② B、①③ C、②③ D、①②③

查看试题解析

8. 如图，在平面直角坐标系中，一块墨迹遮挡了横轴的位置，只留下部分纵轴和部分正方形网格，该网格的每个小正方形的边长都是2个单位长度，每个小正方形的顶点叫格点．若格点A、B在函数 $y = \frac{k}{x} (x > 0)$ 的图象上，则k的值为（）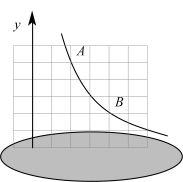

A、6 B、12 C、24 D、48

查看试题解析

二、填空题

9. “抛掷一枚质地均匀的硬币，结果正面朝上”是事件（选填“随机”或“必然”）.

查看试题解析
10. 为了解某市八年级学生的身高情况，从中抽测了1500名学生进行调查，在这次调查中，样本容量是．

查看试题解析
11. 若反比例函数y= $\frac{k - 3}{x}$ 的图象位于一、三象限内，则k的取值范围是．

查看试题解析
12. 若分式 $\frac{3 x - 1}{x^{2} + 1}$ 的值为0，则x的值是．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 3$ ，点 $E$ 在 $A D$ 上， $D E = 1$ ．若 $E C$ 平分 $∠ B E D$ ，则 $B C$ 的长为．

查看试题解析
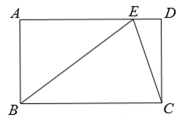14. 数轴上的两个点a，b如图所示，则式子 $a + \sqrt{{(a - b)}^{2}}$ 的值为．

查看试题解析
15. 如图是友谊商场某商品1~4月份单个的进价和售价的折线统计图，则售出该商品单个利润最大的是月份．

查看试题解析
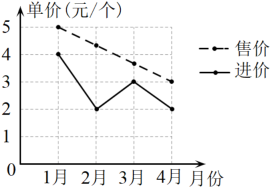16. 如图，从一个大正方形中可以裁去面积为8cm²和32cm²的两个小正方形，则大正方形的边长为．

查看试题解析
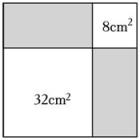17. 如图，正比例函数 $y = k x$ 与函数 $y = \frac{6}{x}$ 的图像交于A，B两点， $B C / / x$ 轴， $A C / / y$ 轴，则 $S_{△ A B C} =$ ．

查看试题解析
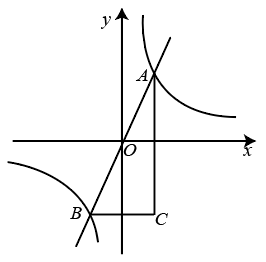18. 如图，在正方形ABCD中，AB=4，AC与BD相交于点O，M是AO的中点，P，Q为对角线BD上的两点，若PQ= $\sqrt{2}$ ，则PM+CQ的最小值为．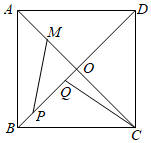

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{m}{m - n} + \frac{n}{n - m}$ ；

(2)、 $\frac{2}{x^{2} - 1} \div \frac{1}{x + 1}$ ．

查看试题解析
20. 计算：

(1)、 $\sqrt{8} + \sqrt{2} - \sqrt{18}$

(2)、 $(\sqrt{3} - 2)^{2}$

查看试题解析
21. 如图，在平面直角坐标系中， $A (3 ， 3) ， B (4 ， 0) ， C (0 ， - 1)$ ．

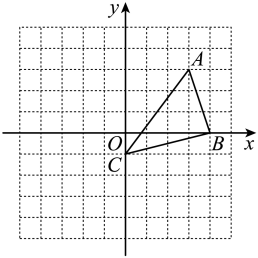(1)、以点C为旋转中心，把 $△ A B C$ 逆时针旋转 $90 °$ ，画出旋转后的图形 $△ A^{'} B^{'} C$ ；

(2)、直接写出 $A^{'}$ ， $B^{'}$ 两点的坐标为 $A^{'}$ ， $B^{'}$ ．

查看试题解析
22. 某校举行学生安全知识竞赛后，从中抽取了部分学生成绩（成绩为正整数，满分为100分）进行统计分析，绘制统计图如下（未全完成）．已知A组的频数比D组小54．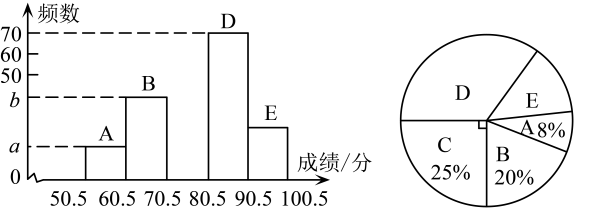
请根据以上信息，解答下列问题：

(1)、频数分布直方图中的 $a =$ ， $b =$ ；

(2)、扇形统计图中D部分所对的圆心角度数为；

(3)、补全频数分布直方图；

(4)、若成绩在80分以上为优秀，全校共有3000名学生，估计成绩优秀的学生有多少名？

查看试题解析
23. 某车间加工1500个零件后，由于技术革新，工作效率提高到原来的 $2.5$ 倍，当再加工同样多的零件时，用时比以前少 $18 h$ ．该车间技术革新前每小时加工多少个零件？

查看试题解析
24. 在 $△ A B C$ 中，点D，F分别为边AC，AB的中点.延长DF到点E，使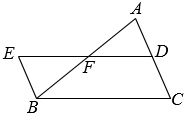 $D F = E F$ ，连接BE.

(1)、求证： $△ A D F ≌ △ B E F$ ；

(2)、求证：四边形BCDE是平行四边形.

查看试题解析
25. 类比和转化是数学中解决新的问题时最常用的数学思想方法．

(1)、【回顾旧知，类比求解】
解方程： $\sqrt{x + 1} = 2$ ．
解：去根号，两边同时平方得一元一次方程，解这个方程，得 $x =$ ．
经检验， $x =$ 是原方程的解．

(2)、【学会转化，解决问题】
运用上面的方法解下列方程：
① $\sqrt{x - 2} - 3 = 0$ ；
② $\sqrt{4 x^{2} + 5 x} - 2 x = 1$ ．

查看试题解析
26. 对于某些函数，由自变量的大小关系确定函数值的大小关系，不仅可以利用函数的图象判断，也可以用代数的方法判断，这是“数形结合”思想的典型应用．

(1)、已知一次函数 $y = - 2 x + 1$ 的图象上的两点 $A (x_{1} ， y_{1}) ､ B (x_{2} ， y_{2}) ， x_{1} < x_{2}$ ，如何用代数的方法判断 $y_{1} ､ y_{2}$ 的大小关系呢？由点 $A ､ B$ 都在函数图象上，得 $y_{1} = - 2 x_{1} + 1$ ， $y_{2} = - 2 x_{2} + 1$ ，再将 $y_{1} ､ y_{2}$ 作差，按照该思路写出判断过程；

(2)、已知反比例函数 $y = \frac{2}{x}$ 的图象上的两点 $A (x_{1} ， y_{1}) ､ B (x_{2} ， y_{2}) ， x_{1} < x_{2} < 0$ ，仿照（1）中的思路写出 $y_{1} ､ y_{2}$ 的大小关系的判断过程．

查看试题解析
27. 如图，在矩形 $A B C D$ 中，点 $E$ 在边 $A B$ 上， $B C = 4 ， B E = 2$ ，

(1)、请用直尺（不带刻度）和圆规，按下列要求作图：在 $C D$ 的延长线上求作点 $F$ ，使 $F C = F E$ ，连接 $E F ， D F$ ．（要求：保留作图痕迹，不写作法）

(2)、在（1）的条件下：
①求证： $E C$ 平分 $∠ B E F$ ；

②求线段 $C F$ 的长．

查看试题解析
28. 如图1，将函数 $y = \frac{k}{x} (x > 0)$ 的图象T₁向左平移4个单位得到函数 $y = \frac{k}{x + 4} (x > - 4)$ 的图象T₂ ， T₂与y轴交于点 $A (0 ， a)$ ．

(1)、若 $a = 3$ ，求k的值

(2)、如图2，B为x轴正半轴上一点，以AB为边，向上作正方形ABCD，若D、C恰好落在T₁上，线段BC与T₂相交于点E
①求正方形ABCD的面积；
②直接写出点E的坐标．

查看试题解析