江苏省扬州市邗江区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-23 类型:期末考试
一、单选题
-
1. 体育是一个锻炼身体、增强体质、培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形且不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,适合采用全面调查(普查)方式的是( )A、对綦江河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班50名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查3. 下列计算正确的是( )A、 B、 C、 D、4. 菱形具有而矩形不一定具有的性质是( )A、内角和等于360° B、对角相等 C、对边平行且相等 D、对角线互相垂直5. 下列式子中,y是 的反比例函数的是 ( )A、 B、 C、 D、6. 分式中,把的值同时扩大为原来的2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、扩大8倍7. 已知点(-2,a)(2,b)(3,c)在函数(k为常数)的图像上,则下列判断正确的是( )A、a<c<b B、b<a<c C、a<b<c D、c<b<a8. 已知,矩形中, , , 点是线段上的一个动点,将线段绕点逆时针旋转得到 , 过作于点 , 连接 , 取的中点 , 连接 , . 点在运动过程中,下列结论:
2. 下列调查中,适合采用全面调查(普查)方式的是( )A、对綦江河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班50名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查3. 下列计算正确的是( )A、 B、 C、 D、4. 菱形具有而矩形不一定具有的性质是( )A、内角和等于360° B、对角相等 C、对边平行且相等 D、对角线互相垂直5. 下列式子中,y是 的反比例函数的是 ( )A、 B、 C、 D、6. 分式中,把的值同时扩大为原来的2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、扩大8倍7. 已知点(-2,a)(2,b)(3,c)在函数(k为常数)的图像上,则下列判断正确的是( )A、a<c<b B、b<a<c C、a<b<c D、c<b<a8. 已知,矩形中, , , 点是线段上的一个动点,将线段绕点逆时针旋转得到 , 过作于点 , 连接 , 取的中点 , 连接 , . 点在运动过程中,下列结论:
①;②当点和点互相重合时,;③;④ . 正确的有( )个.
A、1 B、2 C、3 D、4二、填空题
-
9. 分式 有意义的条件是 .10. 比较大小: (填“>”或“<”=).11. 一只袋内装有3只红球和2只白球,这5只球除颜色外均相同,5人依次从袋中取一只球后并放回,则第四人摸到白球的概率是 .12. 函数 的图象与直线y=x没有交点,那么k的取值范围是 .
13. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .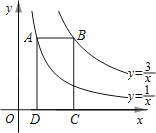 14. 如图,已知菱形的对角线 , 的长分别是 , , , 垂足为点 , 则的长是 .
14. 如图,已知菱形的对角线 , 的长分别是 , , , 垂足为点 , 则的长是 . 15. 若直角三角形的两直角边长为a、b,且满足 则该直角三角形的斜边长为 .16. 关于x的分式方程 的解为正数,则m的取值范围是 .17. 已知关于的代数式有意义,满足条件的所有整数的和是0,则的取值范围为 .18. 如图,点坐标为 , 点坐标为 , 将线段绕点按顺时针方向旋转得到对应线段 , 若点恰好落在轴上,则点的坐标是 .
15. 若直角三角形的两直角边长为a、b,且满足 则该直角三角形的斜边长为 .16. 关于x的分式方程 的解为正数,则m的取值范围是 .17. 已知关于的代数式有意义,满足条件的所有整数的和是0,则的取值范围为 .18. 如图,点坐标为 , 点坐标为 , 将线段绕点按顺时针方向旋转得到对应线段 , 若点恰好落在轴上,则点的坐标是 .
三、解答题
-
19. 计算:(1)、;(2)、 .20. 解下列方程:(1)、(2)、21. 先化简然后请你在中择一个你喜欢的整数代入求值.22. 某县为了了解2013年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向(A.读普通高中; B.读职业高中 C.直接进入社会就业; D.其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).
请问:
 (1)、该县共调查了名初中毕业生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.23. 如图所示,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证OE=BC.
(1)、该县共调查了名初中毕业生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.23. 如图所示,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证OE=BC. 24. 2023年5月19日,慈善一日捐活动中,我校师生积极捐款,已知上午捐款4800元,下午捐款6000元,下午捐款人数比上午捐款人数多50人,且上午和下午的人均捐款数相等,那么当天参加捐款的人数是多少?25. 已知线段 , 请你用圆规和无刻度的直尺作图,需保留作图痕迹.
24. 2023年5月19日,慈善一日捐活动中,我校师生积极捐款,已知上午捐款4800元,下午捐款6000元,下午捐款人数比上午捐款人数多50人,且上午和下午的人均捐款数相等,那么当天参加捐款的人数是多少?25. 已知线段 , 请你用圆规和无刻度的直尺作图,需保留作图痕迹. (1)、请在图1中作以线段为底的等腰;(2)、请在图2中作 .26. 在数学课外学习活动中,小华和他的同学遇到一道题:
(1)、请在图1中作以线段为底的等腰;(2)、请在图2中作 .26. 在数学课外学习活动中,小华和他的同学遇到一道题:已知 , 求的值.小华是这样解答的:
∵ ,
∴ .
请你根据小华的解题过程,解决下列问题.
(1)、填空:=;=;(2)、化简:;(3)、若 , 求的值.27. 问题,我们已经知道反比例函数的图象是双曲线,那么函数的图象是怎样的呢? (1)、该函数的自变量的取值范围为 ;(2)、描点画图:
(1)、该函数的自变量的取值范围为 ;(2)、描点画图:①列表:如表是x与y的几组对应值;
x
…
0
1
2
4
5
6
7
…
y
…
2
3
6
6
3
2
…
②描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点.
③连线:用平滑的曲线顺次连接各点,请你把图象补充完整.
(3)、若点 , 为该函数图象上不同的两点,则;(4)、直接写出当时,x的取值范围为 .28. 如图,正方形中, , 点在边上,且 . 将沿对折至 , 延长交边于点 , 连接、 . (1)、求证:;(2)、求的长;(3)、求的面积;(4)、在的条件下,直接写出周长的最小值.
(1)、求证:;(2)、求的长;(3)、求的面积;(4)、在的条件下,直接写出周长的最小值.