陕西省咸阳市武功县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-23 类型:期末考试
一、单选题
-
1. 某种玫瑰花花粉的直径约为 , 将数据用科学记数法表示为( )A、 B、 C、 D、2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 唐白居易《赋得古原草送别》诗中写道“离离原上草,一岁一枯荣”,从数学的观点看,诗句中描述的事件是( )A、必然事件 B、不可能事件 C、随机事件 D、不属于上述任何一种4. 如图,直线 , 的顶点B在直线上,若 , 则的度数为( )
3. 唐白居易《赋得古原草送别》诗中写道“离离原上草,一岁一枯荣”,从数学的观点看,诗句中描述的事件是( )A、必然事件 B、不可能事件 C、随机事件 D、不属于上述任何一种4. 如图,直线 , 的顶点B在直线上,若 , 则的度数为( )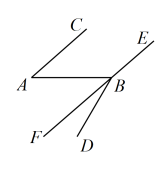 A、100° B、120° C、140° D、160°5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在与中, , 再添加下列哪个条件,能判定( )
A、100° B、120° C、140° D、160°5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在与中, , 再添加下列哪个条件,能判定( )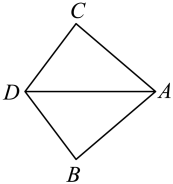 A、 B、 C、DA平分 D、7. 如图1,小亮家、报亭、羽毛球馆在一条直线上,小亮先从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家,小亮离家的距离y与时间x之间的关系如图2所示,下列结论错误的是( )
A、 B、 C、DA平分 D、7. 如图1,小亮家、报亭、羽毛球馆在一条直线上,小亮先从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家,小亮离家的距离y与时间x之间的关系如图2所示,下列结论错误的是( )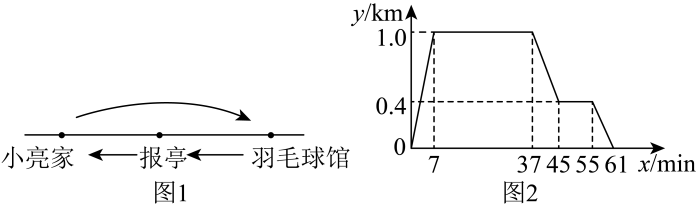 A、小亮从家到羽毛球馆用了7分钟 B、报亭到小亮家的距离是400米 C、小亮在报亭看了10分钟报纸 D、小亮在羽毛球馆打了37分钟羽毛球8. 如图,在中,平分交于点D , 延长到点E , 使得 , 连接 . 若 , 则的度数是( )
A、小亮从家到羽毛球馆用了7分钟 B、报亭到小亮家的距离是400米 C、小亮在报亭看了10分钟报纸 D、小亮在羽毛球馆打了37分钟羽毛球8. 如图,在中,平分交于点D , 延长到点E , 使得 , 连接 . 若 , 则的度数是( )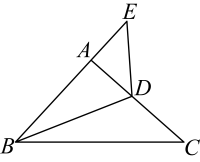 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,要使CDBE , 需要添加的一个条件为: .
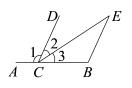 10. 如图,一个可以自由转动的转盘,被分成了9个相同的扇形,转动转盘,转盘停止时,指针落在阴影区域的概率等于 .
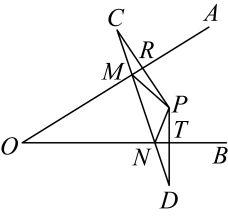
10. 如图,一个可以自由转动的转盘,被分成了9个相同的扇形,转动转盘,转盘停止时,指针落在阴影区域的概率等于 .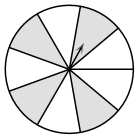 11. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.
11. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.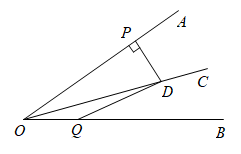 12. 张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x()与售价y(元)之间的关系如下表:
12. 张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x()与售价y(元)之间的关系如下表:重量x/
1
2
3
4
…
售价y/元
…
根据表格中的数据,当卖出柚子的重量为6时,售价为 .
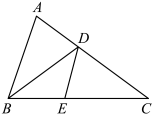
13. 如图,是的角平分线, , 点E在边上,且 , 连接 . 若 , 则的度数为 .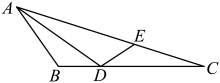
三、解答题
-
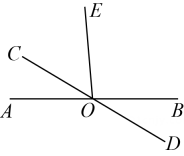
14. 计算: .15. 如图,直线 , 交于点O , , 若 , 求的度数.
 16. 某玩具公司承接了第19届杭州亚运会吉祥物公仔的生产任务,现对一批公仔进行抽检,其结果统计如下:
16. 某玩具公司承接了第19届杭州亚运会吉祥物公仔的生产任务,现对一批公仔进行抽检,其结果统计如下:抽取的公仔数n
10
100
1000
2000
3000
5000
优等品的频数m
9
96
951
1900
2856
4750
优等品的频率
a
b
请根据表中数据,回答问题:
(1)、填空: , ;(2)、从这批公仔中任意抽取1只公仔,估计它是优等品的概率.(精确到)17. 如图,已知 , 利用尺规作图法求作边的垂直平分线 , 分别交、于点M、N . (不写作法,保留作图痕迹)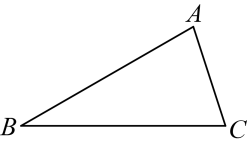 18. 如图,在和中,点A、B、C在一条直线上, , , . 试说明:点C是的中点.
18. 如图,在和中,点A、B、C在一条直线上, , , . 试说明:点C是的中点.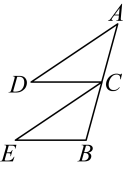 19. 如图,以直线l为对称轴在网格中画出图形的另一半.
19. 如图,以直线l为对称轴在网格中画出图形的另一半. 20. 先化简再求值: , 其中 , .21. 如图,、两建筑物位于河的两岸,要测得它们之间的距离,可以从点出发沿河岸画一条射线 , 在上截取 , 过作 , 使点、、在同一直线上,则的长就是、之间的距离,请你说明理由.
20. 先化简再求值: , 其中 , .21. 如图,、两建筑物位于河的两岸,要测得它们之间的距离,可以从点出发沿河岸画一条射线 , 在上截取 , 过作 , 使点、、在同一直线上,则的长就是、之间的距离,请你说明理由.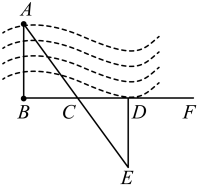 22. 已知一个长方形相邻的两边长分别是x和4 , 设长方形的周长为y .(1)、请写出y与x之间的关系式;(2)、当时,求长方形的周长;(3)、当长方形周长为30时,求x的值.23. 已知等腰三角形的三边长分别为 , , 8,求等腰三角形的周长.24. 一个不透明的袋中装有红、黄、白三种颜色的小球,它们除颜色不同外其余都相同,其中红球有10个,黄球有6个,白球有4个,搅匀袋中的球.(1)、随机地从袋中摸出1个球,求摸到白球的概率;(2)、随机地从袋中摸出1个球,求摸到黄球或红球的概率;(3)、若先从袋中取出2个红球和2个白球,将它们放在桌上,再随机地从袋中摸出1个球,求这时摸到白球的概率.
22. 已知一个长方形相邻的两边长分别是x和4 , 设长方形的周长为y .(1)、请写出y与x之间的关系式;(2)、当时,求长方形的周长;(3)、当长方形周长为30时,求x的值.23. 已知等腰三角形的三边长分别为 , , 8,求等腰三角形的周长.24. 一个不透明的袋中装有红、黄、白三种颜色的小球,它们除颜色不同外其余都相同,其中红球有10个,黄球有6个,白球有4个,搅匀袋中的球.(1)、随机地从袋中摸出1个球,求摸到白球的概率;(2)、随机地从袋中摸出1个球,求摸到黄球或红球的概率;(3)、若先从袋中取出2个红球和2个白球,将它们放在桌上,再随机地从袋中摸出1个球,求这时摸到白球的概率.