陕西省延安市富县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-23 类型:期末考试
一、单选题
-
1. 下列能构成直角三角形的是( )A、1,1,1 B、2,3,4 C、3,4,5 D、3,5,72. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 在平行四边形中,若 , 则的度数为( )A、 B、 C、 D、4. 某便利店7天销售一类货品的销量(单位:件)分别为5,6,7,5,8,10,6,该组数据的中位数是( )A、5 B、7 C、6.5 D、65. 若直线与相交于点 , 则的值为( )A、 B、 C、 D、86. 如图,四边形ABCD是平行四边形,对角线AC , BD相交于点O , 添加下列条件后仍不能判定这个四边形是矩形的是( )
 A、 B、 C、 D、7. 如图,在平面直角坐标系中,点A坐标为 , 以点O为圆心,的长为半径画弧,交x轴的正半轴于点B , 则点B的横坐标介于( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,点A坐标为 , 以点O为圆心,的长为半径画弧,交x轴的正半轴于点B , 则点B的横坐标介于( ) A、5和6之间 B、7和8之间 C、10和11之间 D、8和9之间8. 若一次函数在的范围内的最大值比最小值大 , 则下列说法正确的是( )A、的值为或 B、的值随的增大而增大 C、该函数图象经过第一、二、三象限 D、在的范围内,的最大值为3
A、5和6之间 B、7和8之间 C、10和11之间 D、8和9之间8. 若一次函数在的范围内的最大值比最小值大 , 则下列说法正确的是( )A、的值为或 B、的值随的增大而增大 C、该函数图象经过第一、二、三象限 D、在的范围内,的最大值为3二、填空题
-
9. 甲、乙两人参加射击比赛的平均成绩都为8环,甲的方差为8.5,乙的方差为7.6,则射击成绩更稳定的是 .10. 为整数,则正整数n的最小值为 .11. 若一次函数的函数值y随x的增大而增大,则k的取值范围是.12. 如图,四边形是平行四边形,若 , , , 则 .
 13. 如图,在菱形中,线段在对角线上运动, , , , 则周长的最小值为 .
13. 如图,在菱形中,线段在对角线上运动, , , , 则周长的最小值为 .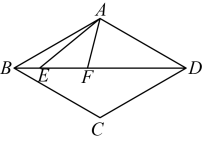
三、解答题
-
14. 计算: .15. 计算: .16. 如图,在正方形中,点 , 分别在 , 边上, , 连接 , 交于点 , 求证: .
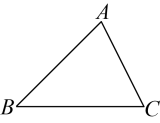
 17. 已知 , 求作边上的中线 . 小明的作法如下:
17. 已知 , 求作边上的中线 . 小明的作法如下:①分别以点 , 为圆心, , 长为半径作弧,两弧相交于点;
②连接 , 与交于点,线段就是所求作的中线.
请你判断小明的作法是否正确,若正确,请使用直尺和圆规补全图形(保留作图痕迹);若不正确,说明理由.
 18. 如图,一次函数的图象经过点 , .
18. 如图,一次函数的图象经过点 , . (1)、求该一次函数的解析式(2)、点该函数的图象上.(填“在”或“不在”)19. 在一次函数中,与的部分对应值如下表:
(1)、求该一次函数的解析式(2)、点该函数的图象上.(填“在”或“不在”)19. 在一次函数中,与的部分对应值如下表: (1)、在平面直角坐标系中,画出这个函数的图象.(2)、观察图象,直接写出当时,的取值范围.20. 某社区随机抽查了该社区内5户居民某天的用电量(单位:度),数据如下表:
(1)、在平面直角坐标系中,画出这个函数的图象.(2)、观察图象,直接写出当时,的取值范围.20. 某社区随机抽查了该社区内5户居民某天的用电量(单位:度),数据如下表:户名
电量
(1)、这5户居民用电量的众数是 .(2)、求这5户居民这天用电量的平均数.21. 如图,点A处的居民楼与马路相距30米,当居民楼与马路上行驶的汽车的距离在50米内时就会受到噪音污染.如果汽车以每秒20米的速度行驶经过,那么会给这栋居民楼带来多长时间的噪音污染? 22. 甲、乙从地出发到达地,甲先出发,中途休息片刻后继续原速前进,随后乙骑自行车出发.如图, , 分别表示甲与乙的路程(千米)随时间(分钟)变化的图象.
22. 甲、乙从地出发到达地,甲先出发,中途休息片刻后继续原速前进,随后乙骑自行车出发.如图, , 分别表示甲与乙的路程(千米)随时间(分钟)变化的图象. (1)、求甲休息完后直线的函数解析式.(2)、乙花多长时间到达地?23. 近年来,各种火灾事故频繁发生,掌握好消防安全知识,可以在火灾发生时起到重要作用.某校为了解学生对消防安全知识的掌握情况,对八年级共1500名同学进行了测试,现随机抽取八(1)班、八(2)班各15名同学的测试成绩(单位:分)进行整理,得到如下信息:
(1)、求甲休息完后直线的函数解析式.(2)、乙花多长时间到达地?23. 近年来,各种火灾事故频繁发生,掌握好消防安全知识,可以在火灾发生时起到重要作用.某校为了解学生对消防安全知识的掌握情况,对八年级共1500名同学进行了测试,现随机抽取八(1)班、八(2)班各15名同学的测试成绩(单位:分)进行整理,得到如下信息:八(1)班15名学生测试成绩:78,83,85,87,89,90,92,93,94,95,97,98,99,100,100
八(2)班15名学生测试成绩其中有1人,有2人,有3人,有5人,有4人
八(1)和八(2)班测试成绩的平均数,中位数,众数,方差如下表所示:
班级
平均数
众数
中位数
方差
八(1)班
92
▲
▲
八(2)班
90
87
91
(1)、根据以上信息,补充完整表格中 , 的信息.(2)、若规定测试成绩90分及以上为优秀,请估计参加测试的1500名学生中成绩为优秀的学生共有多少人?(3)、根据以上数据,你认为哪个班的学生消防安全知识测试的整体成绩更好?请说明理由.24. 如图,在中,分别为的中点,延长至点 , 使 , 连接交于点 . (1)、求证:四边形为平行四边形.(2)、若 , 求的长.25. 某批发市场计划购进A , B两种型号课桌共150张,这两种课桌的进价和售价如下表所示:
(1)、求证:四边形为平行四边形.(2)、若 , 求的长.25. 某批发市场计划购进A , B两种型号课桌共150张,这两种课桌的进价和售价如下表所示:进价(元/张)
售价(元/张)
A
40
50
B
55
70
设购进A种型号课桌x张,销售完这150张课桌共获利润y元.
(1)、求y与x的函数解析式.(2)、该批发市场预计进货款为6900元,求销售完这两种型号课桌获得的利润.26.(1)、问题提出在平面内,已知线段 , , 则线段的最小值为 .
(2)、问题探究如图1,在平行四边形中, , , , P是边的中点,Q是边上一动点,将三角形沿所在直线翻折,得到三角形 , 连接 , 求的最小值.
(3)、问题解决如图2,平行四边形为某公园平面示意图,扇形为该公园的人口广场,已知 , , , . 为了提升游客体验感,工作人员准备在弧上找一点P , 沿 , 修两条绿色通道,并在上方和右方区域种植花卉供游客观赏,其余地方修建其他设施,求其他设施区域面积的最小值.
