（第一次学期单元测试）第1章有理数—2023-2024学年浙教版七年级数学

试卷更新日期：2023-08-22 类型：单元试卷

进入出卷网下载

一、选择题

1. 大于-1且小于2的整数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. $- \frac{2}{3}$ 的绝对值是（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
3. $- \frac{1}{3}$ 的相反数是（）

A、 $- 3$ B、3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
4. 数轴上表示﹣5的点到原点的距离为（　　）

A、5 B、-5 C、 $\frac{1}{5}$ D、- $\frac{1}{5}$

查看试题解析
5. 我国古代《九章算术》中注有“今两算得失相反，要令正负以名之”.是今有两数若其意义相反，则分别叫做正数与负数，如果向北走 $5$ 步记作 $+ 5$ 步，那么向南走 $10$ 步记作（　　）

A、 $+ 10$ 步 B、 $- 10$ 步 C、 $+ 12 步$ D、 $- 2$ 步

查看试题解析
6. 中国古代著作《九章算术》在世界数学史上首次正式引入负数．若小文同学通过微信抢红包“收入” $8.8$ 元，记作“ $+ 8.8$ 元”，则他用微信消费 $5.8$ 元应记作（）

A、 $+ 5.8$ 元 B、 $- 5.8$ 元 C、 $+ 3$ 元 D、 $- 3$ 元

查看试题解析
7. 若a－|a|＝－20，则实数a在数轴上的对应点一定在（）

A、原点左侧 B、原点或原点左侧 C、原点右侧 D、原点或原点右侧

查看试题解析
8. 若lal=3，lbl=5，a与b异号，则|a-b|的值为（）

A、2 B、-2 C、8 D、2或8

查看试题解析
9. 在生产图纸上通常用 $\emptyset 30 0_{- 0.5}^{+ 0.2}$ 来表示轴的加工要求，这里 $\emptyset 300$ 表示直径是 $300 m m$ ， $+ 0.2$ 和 $- 0.5$ 是指直径在 $(300 - 0.5) m m$ 到 $(300 + 0.2) m m$ 之间的产品都属于合格产品.现加工一批轴，尺寸要求是 $\emptyset 4 5_{- 0.3}^{+ 0.2}$ ，则下面产品合格的是（）

A、 $44.6 m m$ B、 $44.8 m m$ C、 $45.3 m m$ D、 $45.5 m m$

查看试题解析
10. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如： $x - y - | z - m | - n = x - y - z + m - n$ ， $| x - y | - z - | m - n | = x - y - z - m + n$ ， ……．
下列说法：

①存在“绝对操作”，使其运算结果与原多项式相等；

②不存在“绝对操作”，使其运算结果与原多项式之和为 $0$ ；

③所有的“绝对操作”共有 $7$ 种不同运算结果．

其中正确的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题

11. 2023的相反数是．

查看试题解析
12. 计算 $2 - | - 3 |$ 的结果为．

查看试题解析
13. 在数轴上，点 $A$ 表示的数为 $- 15$ ，点 $M$ 以每秒3个单位长度的速度从点 $A$ 出发沿数轴向右运动经过秒，点 $M$ 与原点 $O$ 的距离为6个单位长度.

查看试题解析
14. 如图，数轴上的点 $A 、 B$ 分别对应实数 $a 、 b$ ，则 $a + b$ 0.（用“>”“<”或“=”填空）

查看试题解析
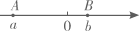15. 若火箭发射点火前5秒记作-5秒，则火箭发射点火后10秒应记作.

查看试题解析
16. 小明写作业时不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的所有整数的和是.

查看试题解析

三、解答题

17. 把下列各数填入相应的集合里：
0.236， $\frac{1}{2}$ ， $- \frac{π}{2}$ ， 0， $\frac{22}{7}$ ， $- 2^{2}$ ， 2023，-0.030030003…
正数集合：{                        …}；
负数集合：{                        …}；
有理数集合：{                        …}；
无理数集合：{                        …}．

查看试题解析
18. 把下列各数表示到数轴上．
$- 1 \frac{1}{3}$ ， 0 ， $- 2^{2}$ ， $- (- 3)$ ， $| - 1 |$

查看试题解析
19. 一天，某出租车被安排以A地为出发地，只在东西方向道路上营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10．假设该出租车每次乘客下车后，都在停车地等待下一个乘客，直到下一个乘客上车再出发．

(1)、将最后一名乘客送到目的地，出租车在A地何处？

(2)、若每千米的价格为3元，司机当天的营业额是多少?

查看试题解析
20. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就点C是(A，B)的美好点例如：如图1，点A表示的数为-1，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是(A，B)的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是〔A，B)的美好点，但点D是(B，A)的美好点。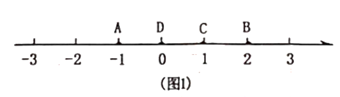

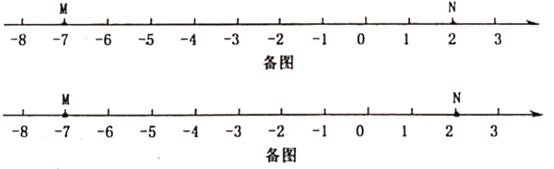
如图2，M，N为数轴上两点，点M所表示的数为-7，点N所表示的数为2.

(1)、点E，F，G表示的数分别是-3，6.5，11，其中是(M，N)美好点的是；写出(N，M)美好点H所表示的数是。

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动.当t为何值时，P，M和N中恰有一个点为其余两点的美好点?

查看试题解析
21. 如图，将一根木棒放在数轴（单位长度为 $1 cm$ ）上，木棒左端与数轴上的点 $A$ 重合，右端与数轴上的点 $B$ 重合.

(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点 $B$ 时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点 $A$ 时，它的左端在数轴上所对应的数为3，由此可得这根木棒的长为 $cm$ ；

(2)、图中点 $A$ 所表示的数是，点 $B$ 所表示的数是；

(3)、受（1）（2）的启发，请借助“数轴”这个工具解决下列问题：
一天，小明去问爷爷的年龄，爷爷说：“我若是你现在这么大，你还要37年才出生；你若是我现在这么大，我就119岁啦！”求爷爷和小明的年龄.

查看试题解析
22. 如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走均为正，向下向左走均为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．

(1)、图中A→C（，），B→C（，），C→（+1，﹣2）；

(2)、若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；

(3)、若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

(4)、若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记为什么？

查看试题解析
23. 在数学问题中，我们常用几何方法解决代数问题，借助数形结合的方法使复杂问题简单化.
材料一：我们知道|a|的几何意义是：数轴上表示数a的点到原点的距离；|a﹣b|的几何意义是：数轴上表示数a，b的两点之间的距离；|a+b|的几何意义是：数轴上表示数a，﹣b的两点之间的距离；根据绝对值的几何意义，我们可以求出以下方程的解.

（ 1 ）|x﹣3|＝4

解：由绝对值的几何意义知：

在数轴上x表示的点到3的距离等于4

∴x₁＝3+4＝7，x₂＝3﹣4＝﹣1

（ 2 ）|x+2|＝5

解：∵|x+2|＝|x﹣（﹣2）|，∴其绝对值的几何意义为：在数轴上x表示的点到﹣2的距离等于5.∴x₁＝﹣2+5＝3，x₂＝﹣2﹣5＝﹣7

材料二：如何求|x﹣1|+|x+2|的最小值.

由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和，要使和最小，则表示数x的这点必在﹣2和1之间（包括这两个端点）取值.

∴|x﹣1|+|x+2|的最小值是3；由此可求解方程|x﹣1|+|x+2|＝4，把数轴上表示x的点记为点P，由绝对值的几何意义知：当﹣2≤x≤1时，|x﹣1|+|x+2|恒有最小值3，所以要使|x﹣1|+|x+2|＝4成立，则点P必在﹣2的左边或1的右边，且到表示数﹣2或1的点的距离均为0.5个单位.

故方程|x﹣1|+|x+2|＝4的解为：x₁＝﹣2﹣0.5＝﹣2.5，x₂＝1+0.5＝1.5.

阅读以上材料，解决以下问题：

(1)、填空：|x﹣3|+|x+2|的最小值为；

(2)、已知有理数x满足：|x+3|+|x﹣10|＝15，有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小，求x﹣y的值.

(3)、试找到符合条件的x，使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小，并求出此时的最小值及x的取值范围.

查看试题解析

（第一次学期单元测试）第1章 有理数—2023-2024学年浙教版七年级数学

一、选择题

二、填空题

三、解答题

（第一次学期单元测试）第1章有理数—2023-2024学年浙教版七年级数学