2023-2024学年北师大版八年级数学上册单元测试 第一章 勾股定理 (B卷)
试卷更新日期:2023-08-22 类型:单元试卷
一、选择题(共10小题,每小题3跟,共30分)
-
1. 将直角三角形的三条边长做如下变化,得到的新三角形仍是直角三角形的是( )A、同加一个相同的数 B、同减一个相同的数 C、同乘以一个相同的正整数 D、同时平方2. 如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若 , 点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为( )
 A、4米 B、4.5米 C、5米 D、5.5米3. 在 中,的对边分别为 , 下列所给数据中, 能判断是直角三角形的是( )A、 B、 C、 D、4. △ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )A、a2+b2=c2 B、∠A=∠B+∠C C、∠A∶∠B∶∠C=3∶4∶5 D、a=5,b=12,c=135. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( )
A、4米 B、4.5米 C、5米 D、5.5米3. 在 中,的对边分别为 , 下列所给数据中, 能判断是直角三角形的是( )A、 B、 C、 D、4. △ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是( )A、a2+b2=c2 B、∠A=∠B+∠C C、∠A∶∠B∶∠C=3∶4∶5 D、a=5,b=12,c=135. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( ) A、4.8 B、5 C、5.8 D、66. 在等腰中, , , 则底边上的高为( )A、12 B、 C、 D、187. 如图所示,已知中, , , 于 , 为上任一点,则 等于( )
A、4.8 B、5 C、5.8 D、66. 在等腰中, , , 则底边上的高为( )A、12 B、 C、 D、187. 如图所示,已知中, , , 于 , 为上任一点,则 等于( )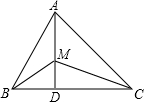 A、9 B、35 C、45 D、无法计算8. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( )
A、9 B、35 C、45 D、无法计算8. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( ) A、 B、 C、 D、9. 如图,在中, , 于点D,E是上一点,且 , 若 , , 则的长为( )
A、 B、 C、 D、9. 如图,在中, , 于点D,E是上一点,且 , 若 , , 则的长为( ) A、 B、 C、 D、10. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( )
A、 B、 C、 D、10. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( ) A、 B、 C、6 D、
A、 B、 C、6 D、二、填空题(共5小题,每小题3分,共15分)
-
11. 如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是.
 12. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.
12. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.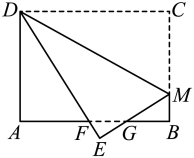 13. 如图,有一张直角三角形的纸片,.现将三角形折叠,使得边与重合,折痕为.则长为.
13. 如图,有一张直角三角形的纸片,.现将三角形折叠,使得边与重合,折痕为.则长为. 14. 如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,米,则BE=米.
14. 如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,米,则BE=米.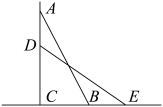 15. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.
15. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.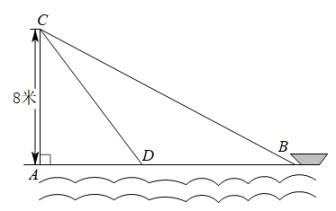
三、解答题(第16题10分,第17-18题每题7分,第19-21每题9分,第22-23每题12分,满分75分)
-
16. 在5×5的正方形网格中,点A,点B均在格点上,连结AB,请根据要求完成下列作图:
 (1)、在图1中找一个格点C,使得△ABC是直角三角形.(2)、在图2中找一个格点D,使得△ABD是三个内角都是锐角的等腰三角形.17. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
(1)、在图1中找一个格点C,使得△ABC是直角三角形.(2)、在图2中找一个格点D,使得△ABD是三个内角都是锐角的等腰三角形.17. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处? 18. 某地一楼房发生火灾,消防队员决定用消防车上的云梯救人如图(1).如图(2),已知云梯最多只能伸长到(即),消防车高 , 救人时云梯伸长至最长,在完成从(即)高的处救人后,还要从(即)高的处救人,这时消防车从处向着火的楼房靠近的距离为多少米?(延长交于点 , , 点在上,的长即为消防车的高)
18. 某地一楼房发生火灾,消防队员决定用消防车上的云梯救人如图(1).如图(2),已知云梯最多只能伸长到(即),消防车高 , 救人时云梯伸长至最长,在完成从(即)高的处救人后,还要从(即)高的处救人,这时消防车从处向着火的楼房靠近的距离为多少米?(延长交于点 , , 点在上,的长即为消防车的高)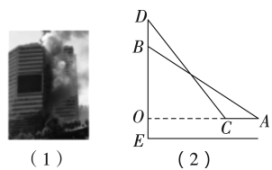 19. 如图,在中, , 平分交于点D,作于点E.
19. 如图,在中, , 平分交于点D,作于点E. (1)、若 , 求的度数;(2)、若 , , 求的面积.20. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB .
(1)、若 , 求的度数;(2)、若 , , 求的面积.20. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB .
(1)、求修建的公路CD的长;(2)、若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?21. 定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. (1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.22. 在△ABC中,AB=AC,∠BAC=90°. 过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD,直线BD交直线AP于点E.
(1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.22. 在△ABC中,AB=AC,∠BAC=90°. 过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD,直线BD交直线AP于点E. (1)、依题意补全图1;(2)、在图1中,若∠PAC=30°,求∠ABD的度数;(3)、若直线AP旋转到如图2所示的位置,请用等式表示线段EB,ED,BC之间的数量关系,并证明.23.
(1)、依题意补全图1;(2)、在图1中,若∠PAC=30°,求∠ABD的度数;(3)、若直线AP旋转到如图2所示的位置,请用等式表示线段EB,ED,BC之间的数量关系,并证明.23. (1)、观察猜想,如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;(2)、问题解决,如图②,在Rt△ABC中,∠ABC=90°,CB=6,AB=3,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;(3)、拓展延伸,如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=6,AB=3,DC=DA,请直接写出BD的长.
(1)、观察猜想,如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;(2)、问题解决,如图②,在Rt△ABC中,∠ABC=90°,CB=6,AB=3,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;(3)、拓展延伸,如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=6,AB=3,DC=DA,请直接写出BD的长.