2023-2024学年北师大版八年级数学上册单元测试卷第一章勾股定理（A卷）

试卷更新日期：2023-08-22 类型：单元试卷

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分

1. 已知 $△ A B C$ 的三条边分别为a，b，c，下列条件不能判断是直角三角形的是（）

A、 $a^{2} = b^{2} - c^{2}$ B、 $a = 6$ ， $b = 8$ ， $c = 10$ C、 $∠ A = ∠ B + ∠ C$ D、 $∠ A ： ∠ B ： ∠ C = 5 ： 12 ： 13$

查看试题解析
2. 以下列各组数为边长，能构成直角三角形的是（）

A、 $\sqrt{3}$ ， $\sqrt{5}$ ， 2 B、1，2， $\sqrt{7}$ C、1， $\sqrt{2}$ ， $\sqrt{3}$ D、4，5，6

查看试题解析
3. 图中字母所代表的正方形的面积为175的选项为（）

A、 B、 C、 D、

查看试题解析
4. 如图，一根长为 $5 m$ 的竹竿 $A B$ 斜靠在竖直的墙壁上，竹竿底端B离墙壁距离 $3 m$ ，则该竹竿的顶端A离地竖直高度为（）

A、 $2 m$ B、 $3 m$ C、 $4 m$ D、 $\sqrt{3} m$

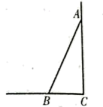查看试题解析
5. 有一直角三角形纸片，∠C＝90°BC＝6，AC＝8，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则CE的长为（）

A、 $2 \sqrt{7}$ B、 $\frac{7}{4}$ C、 $\frac{7}{2}$ D、4

查看试题解析
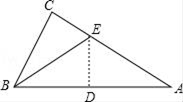6. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，分别以AC，BC，AB为边在三角形外部作正方形．若以AC和BC为边的正方形面积分别为5和3，则以AB为边的正方形面积S的值为（）

A、4 B、8 C、 $2 \sqrt{2}$ D、34

查看试题解析
7. 分别以下列四组数作为三角形的边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{6}$ C、2，3，4 D、9，12，15

查看试题解析
8. 如图，在“庆国庆，手拉手”活动中，某小组从营地A出发，沿北偏东 $53 °$ 方向走了1200m到达B点，然后再沿北偏西 $37 °$ 方向走了500m到达目的地C点，此时A，C两点之间的距离为（）

A、1000m B、1100m C、1200m D、1300m

查看试题解析
9. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ 交AC于点D，且 $B D ⊥ A C$ ， F在BC上，E为AF的中点，连接DE，若 $B F = D E$ ， $A C = 2 \sqrt{3} D E$ ， $B D = 6$ ，则AB的长为（）

A、 $3 \sqrt{6}$ B、 $4 \sqrt{3}$ C、 $\sqrt{42}$ D、9

查看试题解析
10. 图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的.若AC＝6，BC＝5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（）

A、51 B、49 C、76 D、无法确定

查看试题解析

二、填空题（共5小题，每小题3分，共15分

11. 直角三角形两条边长分别为3和4，则第三边的长为.

查看试题解析
12. 如图， $D$ 为 $R t △ A B C$ 中斜边 $B C$ 上的一点，且 $B D = A B$ ，过点 $D$ 作 $B C$ 的垂线，交 $A C$ 于点 $E$ ，若 $A E = 6 c m$ ， $D C = 8 c m$ ，则 $C E =$ $c m$ .

查看试题解析
13. 已知一个三角形的三边长分别是4cm、7cm、6cm，该三角形的形状（填“是”或“不是”）直角三角形．

查看试题解析
14. 如图是一个滑梯示意图，左边是楼梯，右边是滑道，已知滑道 $A C$ 与 $A E$ 的长度相等，滑梯的高度 $B C = 6 m$ ， $B E = 2 m$ .则滑道 $A C$ 的长度为m.

查看试题解析
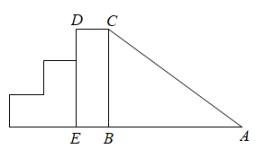15. 如图所示的衣架可以近似看成一个等腰三角形ABC，其中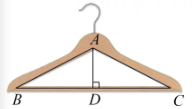 $A B = A C = 25 c m$ ，底边BC的长 $48 c m$ ，那么衣架的高 $A D =$ $c m$ .

查看试题解析

三、解答题（16题10分，17-18每题7分，19-21每题9分，22-23每题12分，满分75分

16. 如图，在长方形纸片ABCD中，AB＝CD＝5，AD＝BC＝3.

(1)、尺规作图：在边BC找一点P，使得△ABP沿直线AP折叠时，B点恰好落在边CD上：（写出作法过程，保留作图痕迹，不需证明）

(2)、求BP的长.

查看试题解析
17. 如图，有两棵树，一棵高6m，另一棵高2m，两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了多少米？（结果精确到0.1m）

查看试题解析
18. 已知：如图，四边形ABCD中，∠ACB=90°，AB=15，BC=9，AD=5，DC=13，
求证：△ACD是直角三角形.

查看试题解析
19. 如图，在 $Δ A B C$ 中， $A D ⊥ B C$ ，垂足为点 $D$ ， $A B = 13$ ， $B D = 5$ ， $A C = 15$ .

(1)、求 $A D$ 的长；

(2)、求 $B C$ 的长.

查看试题解析
20. 如图， $A D ⊥ B C$ ，垂足为 $D$ . 如果 $C D = 1 ， A D = 2 ， B D = 4$ ，

(1)、直接写出 $A C^{2} =$ ， $A B^{2} =$ ；

(2)、 $Δ A B C$ 是直角三角形吗？证明你的结论.

查看试题解析
21. 如图，网格中每个小正方形的边长都是1，点A、B、C、D都在格点上．

(1)、线段AB的长度是，线段CD的长度是．

(2)、若EF的长为 $\sqrt{5}$ ，那么以AB、CD、EF三条线段为边能否构成直角三角形，并说明理由．

查看试题解析
22. 如图，点A在直线l上，在直线l右侧做等腰三角形 $A B C$ ， $A B = A C$ ， $∠ B A C = α$ ，点D与点B关于直线l轴对称，连接 $C D$ 交直线l于点E，连接 $B E$ .

(1)、求证： $∠ A D C = ∠ A C D$ ；

(2)、求证： $∠ B E C = α$ ；

(3)、当 $α = 90 °$ 时，求证： $E D^{2} + C E^{2} = 2 A B^{2}$ .

查看试题解析
23. 综合与探究
已知在 $R t △ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ， D为直线 $B C$ 上一动点（点D不与点B，点C重合），以 $A D$ 为边作 $R t △ A D E$ （其中 $A D = A E ， ∠ D A E = 90 °$ ），连接 $C E$ ．

(1)、如图1，当点D在边 $B C$ 上时，求 $∠ D C E$ 的度数．

(2)、如图2，当点D在边 $B C$ 的延长线上运动时，类比第（1）问，请你猜想线段 $B D$ ， $C D$ ， $D E$ 的数量关系，并说明理由．

(3)、如图3，当点D在边 $C B$ 的延长线上时， $A C = \sqrt{2} ， C E = 1$ ，求线段 $D E$ 的长．

查看试题解析

2023-2024学年北师大版八年级数学上册单元测试卷 第一章 勾股定理（A卷）

一、选择题（共10小题，每小题3分，共30分

二、填空题（共5小题，每小题3分，共15分

三、解答题（16题10分，17-18每题7分，19-21每题9分，22-23每题12分，满分75分

2023-2024学年北师大版八年级数学上册单元测试卷第一章勾股定理（A卷）