2023-2024学年北师大版数学八年级上册3.3轴对称与坐标变化（培优卷）

试卷更新日期：2023-08-21 类型：同步测试

进入出卷网下载

一、选择题

1. 在平面直角坐标系 $x O y$ 中，点 $A (- 1 ， 2)$ 关于原点对称的点的坐标是（）

A、 $(1 ， - 2)$ B、 $(- 1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(- 1 ， - 2)$

查看试题解析
2. 如图，在平面直角坐标系中点A的坐标为（3，4），D是△ABC内一点，将△ABC平移得到 $△ A^{'} B^{'} C^{'}$ ，平移后点D与其对应点D'关于x轴对称，设点D的坐标为（a，b），则A的对应点 $A^{'}$ 的坐标为（）

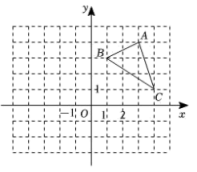A、（3，－4） B、（3，4－2b） C、（3，4－2a） D、（－3，4－2b）

查看试题解析
3. 若点 $A (a ， - 2)$ ， $B (3 ， b)$ 关于x轴对称，则a ， b的值分别为（）

A、 $a = 3$ ， $b = - 2$ B、 $a = - 3$ ， $b = - 2$ C、 $a = 3$ ， $b = 2$ D、 $a = - 3$ ， $b = 2$

查看试题解析
4. 平面直角坐标系中，若点 $A (- 1 ， a)$ 与点 $B (b ， 3)$ 关于x轴对称，则点 $C (a ， b)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 若点P（a，3）与点Q（-2，b）关于坐标原点对称，则a+b的值为（）

A、1． B、-1 C、3 D、-3

查看试题解析
6. 如图，在平面直角坐标系中，△ABC关于直线m（直线m上各点的横坐标都为1）对称，点C的坐标为（4，1），则点B的坐标为（）

A、（-2，1） B、（-3，1） C、（-2，-1） D、（2，1）

查看试题解析
7. 已知点E（x₀ ， y_o），点F（x₂.y₂），点M（x₁ ， y₁）是线段EF的中点，则x₁＝ $\frac{x_{0} + x_{2}}{2}$ ，y₁＝ $\frac{y_{0} + y_{2}}{2}$ .在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P₁（即P，A，P₁三点共线，且PA＝P₁A），P₁关于点B的对称点P₂ ， P₂关于点C的对称点P₃ ， …按此规律继续以A，B，C三点为对称点重复前面的操作.依次得到点P₄ ， P₅ ， P₆…，则点P₂₀₂₀的坐标是（　　）

A、（4，0） B、（﹣2，2） C、（2，﹣4） D、（﹣4，2）

查看试题解析
8. 在平面直角坐标系中，对 $Δ A B C$ 进行循环往复的轴对称变换，若原来点 $A$ 的坐标是 $(\sqrt{3} ， \sqrt{2})$ ，则经过第2019次变换后所得的点 $A$ 的坐标是（）

A、 $(- \sqrt{3} ， \sqrt{2})$ B、 $(- \sqrt{3} ， - \sqrt{2})$ C、 $(\sqrt{3} ， - \sqrt{2})$ D、 $(\sqrt{3} ， \sqrt{2})$

查看试题解析
9. 在平面直角坐标系中，正方形ABCD的顶点分别为A（1，1）.B（1，﹣1）.C（﹣1，﹣1）.D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P₁ ，作P₁关于点B的对称点P₂ ，作点P₂关于点C的对称点P₃ ，作P₃关于点D的对称点P₄ ，作点P₄关于点A的对称点P₅ ，作P₅关于点B的对称点P₆┅，按如此操作下去，则点P₂₀₁₁的坐标为（）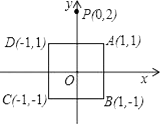

A、（0，2） B、（2，0） C、（0，﹣2） D、（﹣2，0）

查看试题解析
10. 如图，在直角坐标系中，矩形OABC的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为（）

A、（﹣ $\frac{1}{2}$ ， $\frac{13}{5}$ ） B、（﹣ $\frac{2}{5}$ ， $\frac{13}{5}$ ） C、（﹣ $\frac{4}{5}$ ， $\frac{12}{5}$ ） D、（﹣ $\frac{3}{5}$ ， $\frac{12}{5}$ ）

查看试题解析

二、填空题

11. 已知点M（x，y）与点N（﹣2，﹣3）关于x轴对称，则x+y= ．

查看试题解析
12. 已知点 $A (- 2 ， b)$ 与点 $B (a ， 3)$ 关于原点对称，则 $a - b =$ ．

查看试题解析
13. 在平面直角坐标系xOy中，已知点P（﹣2，1）关于y轴的对称点P′，点T（t，0）是x轴上的一个动点，当△P′TO是等腰三角形时，t的值是.

查看试题解析
14. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

查看试题解析
15. 如图，在平面直角坐标中，对抛物线 $y = - 2 x^{2} + 2 x$ 在x轴上方的部分进行循环反复的轴对称或中心对称变换，若点A是该抛物线的顶点，则经过第2020次变换后所得的A点的坐标是．

查看试题解析

三、综合题

16. 点 $P (m + 3 ， 3 - 2 m)$ 与点 $Q (m^{2} - 5 m ， | 2 m - 3 |)$ 在同一平面直角坐标系中．

(1)、若点 $P$ 位于第四象限，求 $m$ 的取值范围；

(2)、若点 $P$ 与点 $Q$ 关于 $y$ 轴对称，求线段 $P Q$ 的长度．

查看试题解析
17. 如图所示，在平面直角坐标系中，已知 $A (2 ， 0)$ 、 $B (0 ， 3)$ 、 $C (3 ， 2)$ ；

(1)、若点 $P$ 与点 $C$ 关于 $x$ 轴对称，则点 $P$ 的坐标为；

(2)、在平面直角坐标系中画出 $△ A B C$ 关于 $y$ 轴对称的图形 $△ D E F$ ；

(3)、已知 $Q$ 为y轴上一点，若 $△ A B Q$ 的面积为2，直接写出点 $Q$ 的坐标.

查看试题解析
18. 如图，在平面直角坐标系中， $△ A B C$ 的顶点均在网格的格点上，其坐标分别为： $A (- 4 ， 4) ， B (- 2 ， 1) ， C (4 ， 2)$ .

(1)、在图中作出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、在(1)的条件下，分别写出点A，C的对应点A₁C₁的坐标.

查看试题解析
19. 如图，在平面直角坐标系 $x O y$ 中，直线l经过点 $M (3 ， 0)$ ，且平行于y轴给出如下定义：点 $P (x ， y)$ 先关于y轴对称得点 $P_{1}$ ，再将点 $P_{1}$ 关于直线l对称得点 $P^{'}$ ，则称点 $P^{'}$ 是点P关于y轴和直线l的二次反射点．

(1)、已知 $A (- 4 ， 0) ， B (- 2 ， 0) ， C (- 3 ， 1)$ ，则它们关于y轴和直线l的二次反射点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标分别是；

(2)、若点D的坐标是 $(a ， 0)$ ，其中 $a < 0$ ，点D关于y轴和直线l的二次反射点是点 $D^{'}$ ，求线段 $D D^{'}$ 的长；

(3)、已知点 $E (4 ， 0)$ ，点 $F (6 ， 0)$ ，以线段 $E F$ 为边在x轴上方作正方形 $E F G H$ ，若点 $P (a ， 1)$ ， $Q (a + 1 ， 1)$ 关于y轴和直线l的二次反射点分别为 $P^{'} ， Q^{'}$ ，且线段 $P^{'} Q^{'}$ 与正方形 $E F G H$ 的边有公共点，求a的取值范围．

查看试题解析
20. 如图，在平面直角坐标系中， $A (- 1 ， 5) ， B (- 1 ， 0) ， C (- 4 ， 3)$ .

(1)、作出 $△ A B C$ 关于 $y$ 轴的对称图形 $△ A' B' C'$ ；

(2)、写出点 $A' ， B' ， C'$ 的坐标.

(3)、在 $y$ 轴上找一点 $P$ ，使 $P A + P C$ 的长最短.

查看试题解析