2023-2024学年北师大版数学八年级上册3.1确定位置 同步练习（培优卷）

试卷更新日期：2023-08-21 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 在学习有序数对时，老师和同学们用如图所示的密码表玩听声音猜动物的游戏．当听到“叮叮-叮，叮叮叮-叮叮，叮-叮”时，分别对应的字母是“C，A，T”，表示的动物是猫．当听到“叮叮-叮叮，叮-叮叮叮，叮叮叮-叮”时，表示的动物是（    ）

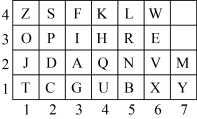    A、牛 B、鱼 C、狗 D、猪

    查看试题解析

  • 2. 在某游乐场，以中心广场为观测点，若有序数对(500 ， 20°)表示图中“太阳神车”的位置，有序数对(400 ， 340°)表示图中“雪域金翅”的位置，则与图中“天地双雄”位置对应的有序数对为（   ）

    A、(500 ， 60°) B、(500 ， 120°) C、(500 ， 100°) D、(400 ， 20°)

    查看试题解析

  • 3. 数经历了从自然数到有理数，到实数，再到复数的发展过程，数学中把形如a+bi（a，b为实数）的数叫做复数，用z＝a+bi表示，任何一个复数z＝a+bi在平面直角坐标系中都可以用有序数对Z（a，b）表示，如：z＝1+2i表示为Z（1，2），则z＝2﹣i可表示为（   ）
    A、Z（2，0） B、Z（2，﹣1） C、Z（2，1） D、（﹣1，2）

    查看试题解析

  • 4. 如图是雷达探测到的6个目标，若目标B用(30，60°)表示，目标D用(50，210°)表示，则表示为(40，120°)的是（ ）

    A、目标A B、目标C C、目标E D、目标F

    查看试题解析

  • 5. 象棋在中国有着三千多年的历史，属于二人对抗性游戏的一种．由于用具简单，趣味性强，成为流行极为广泛的棋艺活动．如图是一方的棋盘，如果“帅”的坐标是(0，1)，“卒”的坐标是(2，2)，那么“马”的坐标是（ ）

    A、(－2，1) B、(2，－2) C、(－2，2) D、(2，2)

    查看试题解析

  • 6. 张明同学的座位位于第2列第5排，李丽同学的座位位于第4排第3列，若张明的座位用有序数对表示为(2 ， 5) ， 则李丽的座位用的有序数对表示为（    ）
    A、(4、3) B、3，4 C、(3 ， 4) D、(4 ， 3)

    查看试题解析

  • 7. 如图甲处表示2街4巷的十字路口，如果用（2，4）表示甲处的位置，那么乙处的位置可以表示为（ ）

    A、（2，4） B、（3，4） C、（4，3） D、（4，2）

    查看试题解析

  • 8. 下列叙述中，不能确定位置的是（ ）
    A、小华在某会场的座位是5排8号 B、某城市位于东经108°，北纬39° C、A城与B城相距15 km D、船C在观测点A北偏东40°方向上30 km处

    查看试题解析

  • 9. 如图是北京市地图简图的一部分，图中“故宫”、“颐和园”所在的区域分别是（   ）

    D

    E

    F

    6

    颐和园

    奥运村

    7

    故宫

    日坛

    8

    天坛
    A、D7，E6 B、D6，E7 C、E7，D6 D、E6，D7

    查看试题解析

  • 10. 小李、小王、小张、小谢原有位置如图（横为排、竖为列），小李在第2排第4列，小王在第3排第3列，小张在第4排第2列，小谢在第5排第4列.撤走第一排，仍按照原有确定位置的方法确定新的位置，下列说法正确的是（   ）.

    A、小李现在位置为第1排第2列 B、小张现在位置为第3排第2列 C、小王现在位置为第2排第2列 D、小谢现在位置为第4排第2列

    查看试题解析

二、填空题

  • 11. 在电影票上将“10排8号”前记为(10 ， 8) ， 那么(25 ， 11)表示的意义是 ．

    查看试题解析

  • 12. 如图，将正整数按如图所示规律排列下去，若用有序数对（m，n）表示m排从左到右第n个数．如（4，3）表示9，则（15，4）表示 ．

    查看试题解析

  • 13. 有一个英文单词的字母顺序对应如图中的有序数对分别为 (3 ， 1) ， (1 ， 2) ， (2 ， 2) ， (7 ， 2) ， (1 ， 1) ，请你把这个英文单词写出来或者翻译中文为 ．

     

    查看试题解析

  • 14. 在2019年迎新联欢会上，数学老师和同学们做了一个游戏. 她在A ， B ， C三个盘子里分别放了一些小球，小球数依次为 a0  ，    b0  ，    c0 ，记为 G0=(a0  ，    b0  ，    c0) . 游戏规则如下：三个盘子中的小球数 a0 ≠b0 ≠c0 ，则从小球最多的一个盘子中拿出两个，给另外两个盘子各放一个，记作一次操作； n 次操作后的小球数记为 Gn=(an  ，    bn  ，    cn) . 若 G0=(3 ，   5 ，   19) ，则 G3= ， G2019= ．

    查看试题解析

  • 15. 如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始，把位于同一列且在拐角处的两个数字提取出来组成有序数对：(3 ， 5)；(7 ， 10)；(13 ， 17)；(21 ， 26)；(31 ， 37)…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究，就会发现其中的规律．请写出第n个数对： ．

      

    查看试题解析

三、综合题

  • 16. 随着科学技术的发展，物流快递已经可以由机器人派送了。机器人能按照设计的指令完成各种动作.在坐标平面上，根据指令{s，a}（s≥0， 0∘<a<180∘ ）机器人能完成下列动作：先原地逆时针旋转角度a，再朝其对面方向沿直线行走距离s.

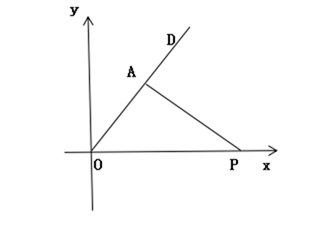    (1)、填空：如图，若机器人在直角坐标系的原点，且面对y轴的正方向，现要使其移动到点A（2，2），则给机器人发出的指令应是（无需过程）；
    (2)、机器人在完成上述指令后，发现在P（ 23+2 ， 0 ）处有一小球正向坐标原点做匀速直线运动，已知小球滚动的速度与机器人行走的速度相同，若忽略机器人原地旋转的时间，请你给机器人发一个指令，使它能刚好截住小球.[第二小题写解题过程]

    查看试题解析

  • 17. 在边长为1的小正方形组成的网格中，把一个点先沿水平方向平移 |a| 格（当 a 为正数时，表示向右平移．当 a 为负数时，表示向左平移），再沿竖直方向平移 |b| 格（当 b 为正数时，表示向上平移．当 b 为负数时，表示向下平移），得到一个新的点，我们把这个过程记为 (a ， b) ．例如，从 A 到 B 记为： A→B(+1 ， +3) ．从 C 到 D 记为： C→D(+1 ， −2) ，回答下列问题：
    (1)、如图1，若点 A 的运动路线为： A→B→C→A ，请计算点 A 运动过的总路程．

    (2)、若点 A 运动的路线依次为： A→M(+2 ， +3) ， M→N(+1 ， −1) ， N→P(−2 ， +2) ， P→Q(+4 ， −4) ．请你依次在图2上标出点 M 、 N 、 P 、 Q 的位置．

    (3)、在图 2 中，若点 A 经过 (m ， n) 得到点 E ，点 E 再经过 (p ， q) 后得到 Q ，则 m 与 p 满足的数量关系是 ． n 与 q 满足的数量关系是 ．

    查看试题解析

  • 18. 如图，蚂蚁在5×5的方格(每个小方格的边长均为1 cm)上沿着网格线运动．它从A处出发去寻找B，C，D处的伙伴，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向，那么图中：

    (1)、A→D( ， )；D→B( ， )；C→B( ， )．
    (2)、若蚂蚁的行走路线为A→B→C→D，请计算蚂蚁走过的路程．
    (3)、若蚂蚁从A处出发去寻找伙伴，它的行走路线依次为(＋1，＋2)，(＋3，－1)，(－2，＋2)，请在图中标出这只蚂蚁伙伴的位置E.
    (4)、在(3)中，若蚂蚁每走1 cm需要消耗1.5焦耳的能量，则蚂蚁在寻找伙伴E的过程中总共需要消耗多少焦耳的能量？

    查看试题解析

  • 19. 阅读：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位，用实数加法表示为3+(-2)=1．若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移 |a| 个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移 |b| 个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．解决问题：

    (1)、计算： {3 ， 1}+{1 ， 2} ，
    (2)、动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C．再按照“平移量”{3，1}平移，最后的位置还是点B．请你在图1中画出四边形OABC；
    (3)、如图2，一艘船从码头O出发，先航行到湖心岛码头P(2，3)，再从码头P航行到码头Q(5，5)，最后回到出发点O．请用“平移量”加法算式表示它的航行过程．

    查看试题解析