（单元测试B卷）第二章对称图形——圆—苏科版2023-2024学年九年级数学上册

试卷更新日期：2023-08-21 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图， $A B$ 是 $⊙ O$ 的直径， $∠ D = 32 °$ ，则 $∠ B O C$ 等于（）

A、32° B、58° C、60° D、64°

查看试题解析
2. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E，连接 $O D$ ，若 $A B = 6$ ， $B E = 1$ ，则弦 $C D$ 的长是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $2 \sqrt{3}$ D、 $2 \sqrt{5}$

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $B C = 4$ .以点A为圆心，r为半径作圆，当点C在 $⊙ A$ 内且点B在 $⊙ A$ 外时，r的值可能是（）

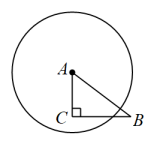A、3 B、4 C、5 D、6

查看试题解析
4. 如图所示，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形， $∠ B C D = 130 °$ ，则 $∠ B O D$ 的大小是（）

A、120° B、110° C、100° D、50°

查看试题解析
5. 如图，圆上有两点 $A$ ， $B$ ，连结 $A B$ ，分别以 $A$ ， $B$ 为圆心， $A B$ 的长为半径画弧，两弧相交于点 $C ， D ， C D$ 交于 $A B$ 点E，交 $\overset{⌢}{A B}$ 于点F，若 $E F = 1 ， A B = 6$ ，则该圆的半径长是（）

A、10 B、6 C、5 D、4

查看试题解析
6. 常用水笔的笔尖是通过顶端的球座口内置一颗可以滚动带墨出水的球珠构成（轴截面如图所示），某工厂生产了一批直径均为 $0.5 m m$ 的球珠和可以放置球珠的笔尖，要求笔头球珠探出部分的长度h不少于 $0.05 m m$ 但不超过 $0.1 m m$ ，以下生产的不同球座口宽度a中符合要求的是（）

A、0.45 B、0.35 C、0.25 D、0.15

查看试题解析
7. 某校举办校庆晚会，其主舞台为一圆形舞台，圆心为O.A，B是舞台边缘上两个固定位置，由线段AB及优弧 $\overset{⌢}{A B}$ 围成的区域是表演区.若在A处安装一台某种型号的灯光装置，其照亮区域如图1中阴影所示.若在B处再安装一台同种型号的灯光装置，恰好可以照亮整个表演区，如图2中阴影所示
若将灯光装置改放在如图3所示的点M，N或P处，能使表演区完全照亮的方案可能是（）
①在M处放置2台该型号的灯光装置②在M，N处各放置1台该型号的灯光装置③在P处放置2台该型号的灯光装置

A、① B、①② C、②③ D、①②③

查看试题解析
8. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，正六边形的周长是12，则 $⊙ O$ 的半径是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{3}$

查看试题解析
9. 图1是一个“不倒翁”，图2是它的主视图， $O A$ ， $O B$ 分别与 $\overset{⌢}{A C B}$ 所在圆相切于点A，B.若该圆半径是8， $∠ O = 54 °$ ，则 $\overset{⌢}{A C B}$ 的长是（）

A、 $2.4 π$ B、 $5.6 π$ C、 $10 π$ D、 $10.4 π$

查看试题解析
10. 如图，圆锥的底面半径 $r = 3$ ，母线 $l = 5$ ，则圆锥的侧面积是（）

A、 $12 π$ B、 $15 π$ C、 $24 π$ D、 $30 π$

查看试题解析

二、填空题（每空3分，共15分）

11. 如图，四边形 $A B C O$ 的顶点 $A$ 、 $B$ 、 $C$ 在 $⊙ O$ 上，若 $∠ A B C = 130 °$ ，则 $∠ A O C =$ .

查看试题解析
12. 如图，A，B、C三点都在 $⊙ O$ 上， $∠ A C B = 35 °$ ，过点A作 $⊙ O$ 的切线与 $O B$ 的延长线交于点P，则 $∠ A P O$ 的度数是．

查看试题解析
13. 如图，用一个半径为6cm的定滑轮拉动砝码上升（假设绳索足够长且粗细不计，与滑轮之间无滑动），若滑轮旋转了 $150 °$ ，则砝码上升了cm.（结果保留 $π$ ）

查看试题解析
14. 如图，圆锥的侧面展开图是一个扇形，若圆锥的底面圆的半径 $r = 2 c m$ ，母线长 $l = 8 c m$ ，则侧面展开图的圆心角 $θ$ 的度数为.

查看试题解析
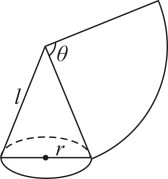15. 如图，半径为4cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P向半径OA引垂线PH交OA于点H.设 $△ O P H$ 的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为.

查看试题解析

三、解答题（共4题，共20分）

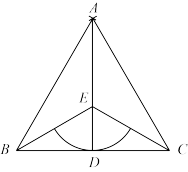
16. 在△ABC中，CE，BD分别是边AB，AC上的高，F是BC边上的中点．

(1)、指出图中的一个等腰三角形，并说明理由．

(2)、若∠A=x°，求∠EFD的度数（用含x的代数式表达）．

(3)、猜想∠ABC和∠EDA的数量关系，并证明．

查看试题解析
17. 如图，已知△ABC，∠B=40°．

(1)、在图中，用尺规作出△ABC的内切圆O，并标出⊙O与边AB，BC，AC的切点D，E，F（保留痕迹，不必写作法）；

(2)、连接EF，DF，求∠EFD的度数．

查看试题解析
18. 如图，正方形ABCD的外接圆为⊙O，点P在劣弧 $\overset{⌢}{C D}$ 上（不与C点重合）．

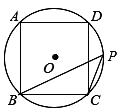(1)、求∠BPC的度数；

(2)、若⊙O的半径为8，求正方形ABCD的边长．

查看试题解析
19. 已知：如图，C，D是以 $A B$ 为直径的半圆周的三等分点， $C D = 8 c m$ .求阴影部分的面积？

查看试题解析

四、综合题（共4题，共20分）

20. 如图， $O A = O B$ ， $A B$ 交 $⊙ O$ 于点 $C$ ， $D$ ， $O E$ 是半径，且 $O E ⊥ A B$ 于点 $F$ .

(1)、求证： $A C = B D$ ；

(2)、若 $C D = 8$ ， $E F = 2$ ，求 $⊙ O$ 的半径.

查看试题解析
21. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C$ 在 $⊙ O$ 上，延长 $B C$ 至点 $D$ ，使 $D C = C B$ .延长 $D A$ 与 $⊙ O$ 的另一个交点为 $E$ ，连结 $A C ， C E$ .

(1)、求证： $∠ D = ∠ E$ ；

(2)、若 $A B = 4 ， B C - A C = 2$ ，求 $C E$ 的长.

查看试题解析
22. 如图，在 $△ A B C$ 中，以边 $A B$ 为直径作 $⊙ O$ 分别交 $B C$ ， $A C$ 于点D，E，点D是 $B C$ 中点，连接 $O E$ ， $O D$ .

(1)、求证： $△ A B C$ 是等腰三角形.

(2)、若 $A B = 6$ ， $∠ A = 40 °$ ，求 $\overset{⌢}{A E}$ 的长和扇形 $E O D$ 的面积.

查看试题解析
23. 如图所示，D是线段BC的中点，分别以点B，C为圆心，BC长为半径画弧，两弧相交于点A，连结AB，AC，AD，E为AD上一点，连结BE，CE.

(1)、求证：BE = CE.

(2)、以点E为圆心作 $\overset{⌢}{F G}$ 与BC相切，分别交BE，CE于点F，G.若BC = 4，∠EBD = 30°，求扇形FEG的面积

(3)、若用扇形FEG围成一个圆锥的侧面，求这个圆锥的底面圆的半径.

查看试题解析

（单元测试B卷）第二章 对称图形——圆—苏科版2023-2024学年九年级数学上册

一、选择题（每题3分，共30分）

二、填空题（每空3分，共15分）

三、解答题（共4题，共20分）

四、综合题（共4题，共20分）

（单元测试B卷）第二章对称图形——圆—苏科版2023-2024学年九年级数学上册