沪科版数学九年级上册第21章二次函数章节过关检测卷
试卷更新日期:2023-08-20 类型:单元试卷
一、选择题
-
1. 已知是y关于x的二次函数,则m的值为( )A、0 B、1 C、4 D、0或42. 抛物线的开口方向、对称轴分别是( ).A、开口向上,对称轴为直线 B、开口向下,对称轴为直线 C、开口向上,对称轴为直线 D、开口向下,对称轴为直线3. 将抛物线向右平移2个单位,再向上平移2个单位,则所得的抛物线的函数表达式为( )A、 B、 C、 D、4. 已知抛物线与x交于点 , , 则关于x的方程的解是( )A、 , B、 , C、 , D、 ,5. 由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )
x
1.0
1.1
1.2
1.3
x2+12x
13
14.41
15.84
17.29
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、14.41<x<15.846. 如图,以40m/s的速度将小球沿与地面成30°角的方向击出后,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t-5t2 . 下列叙述正确的是( ( )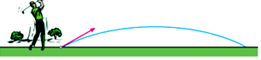 A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m C、小球从飞出到落地要用时4s D、小球飞出1s时的飞行高度为10m7. 商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )A、y=10(200﹣10x) B、y=200(10+x) C、y=10(200﹣10x)2 D、y=(10+x)(200﹣10x)8. 已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( )
A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m C、小球从飞出到落地要用时4s D、小球飞出1s时的飞行高度为10m7. 商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )A、y=10(200﹣10x) B、y=200(10+x) C、y=10(200﹣10x)2 D、y=(10+x)(200﹣10x)8. 已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( ) A、
A、 B、
B、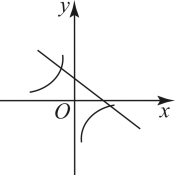 C、
C、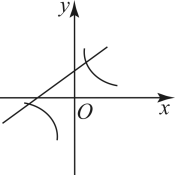 D、
D、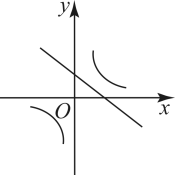 9. 已知二次函数 , 当时,y有最小值和最大值5,则m的取值范围为( )A、 B、 C、 D、10. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
9. 已知二次函数 , 当时,y有最小值和最大值5,则m的取值范围为( )A、 B、 C、 D、10. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 有下列函数:
①y=5x-4;②y=;③y=2x3-8x2+3;④y=x2-1;⑤y=;
其中属于二次函数的是 (填序号).
12. 如果一个二次函数的图象顶点是原点,且它经过平移后能与的图像重合,那么这个二次函数的解析式是 .13. 如图,点A、B是双曲线y= 上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2= 14. 已知二次函数(a是常数,且).(1)、该二次函数图象的对称轴是;(2)、该二次函数图象与y轴交点的纵坐标的最大值为 .
14. 已知二次函数(a是常数,且).(1)、该二次函数图象的对称轴是;(2)、该二次函数图象与y轴交点的纵坐标的最大值为 .三、解答题
-
15. 已知抛物线过点和 , 求该抛物线的解析式.
四、作图题
-
16. 如图,二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,顶点为D.
 (1)、求此二次函数的解析式.(2)、求点D的坐标及△ABD的面积.17. 已知二次函数 .
(1)、求此二次函数的解析式.(2)、求点D的坐标及△ABD的面积.17. 已知二次函数 . (1)、将 化成 的形式为;(2)、此函数与 轴的交点坐标为;(3)、在平面直角坐标系 中画出这个二次函数的图象(不用列表);(4)、直接写出当 时, 的取值范围.
(1)、将 化成 的形式为;(2)、此函数与 轴的交点坐标为;(3)、在平面直角坐标系 中画出这个二次函数的图象(不用列表);(4)、直接写出当 时, 的取值范围.五、综合题
-
18. 已知二次函数(1)、求证:二次函数的图像与x轴总有两个交点(2)、若二次函数的图像与x轴交点的横坐标一个大于2,一个小于1,求m的取值范围.19. 如图,直线为常数与双曲线(为常数)相交于 , 两点.
 (1)、求直线的解析式;(2)、在双曲线上任取两点和 , 若 , 试确定和的大小关系,并写出判断过程;(3)、请直接写出关于的不等式的解集.20. 如图,已知二次函数的图象经过点 .
(1)、求直线的解析式;(2)、在双曲线上任取两点和 , 若 , 试确定和的大小关系,并写出判断过程;(3)、请直接写出关于的不等式的解集.20. 如图,已知二次函数的图象经过点 . (1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点在该二次函数的图象上,若 , 试根据图象直接写出m的取值范围.21. 云南某旅游景区购进一批文创产品,40天销售完毕.根据记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是 , 销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示.
(1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点在该二次函数的图象上,若 , 试根据图象直接写出m的取值范围.21. 云南某旅游景区购进一批文创产品,40天销售完毕.根据记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是 , 销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示. (1)、第15天的日销售量为件;(2)、当时,求日销售额的最大值.22. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 .
(1)、第15天的日销售量为件;(2)、当时,求日销售额的最大值.22. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 . (1)、若一次性燃烧完药物需10分钟.
(1)、若一次性燃烧完药物需10分钟.①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?
(2)、已知室内每立方米空气中的含药量不低于时,才能有效消毒,如果有效消毒时间要持续120分钟,问要一次性燃烧完这种药物需多长时间?23. 已知抛物线交轴于和 , 交轴于. (1)、求抛物线的解析式;(2)、若为抛物线上第二象限内一点,求使面积最大时点的坐标;(3)、若是对称轴上一动点,是抛物线上一动点,是否存在、 , 使以、、、为顶点的四边形是平行四边形?若存在,直接写出点的坐标.
(1)、求抛物线的解析式;(2)、若为抛物线上第二象限内一点,求使面积最大时点的坐标;(3)、若是对称轴上一动点,是抛物线上一动点,是否存在、 , 使以、、、为顶点的四边形是平行四边形?若存在,直接写出点的坐标.
-