2023年浙教版数学九年级上册第四章 相似三角形 章末检测(C卷)
试卷更新日期:2023-08-20 类型:单元试卷
一、选择题(每题2分,共20分)
-
1. 如果 , 则下列式子正确的是( )A、 B、 C、 D、2. 主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上(BP长为x),则x满足的方程是( )
 A、 B、 C、 D、以上都不对3. 如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( )
A、 B、 C、 D、以上都不对3. 如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( ) A、先变长后变短 B、先变短后变长 C、不变 D、先变短后变长再变短4. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).,图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中,以点 B 为圆心,AB 为半径作 AC,再 以CD 为直径作半圆交 AC 于点E,若边长AB=10,则△CDE 的面积为( )
A、先变长后变短 B、先变短后变长 C、不变 D、先变短后变长再变短4. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).,图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中,以点 B 为圆心,AB 为半径作 AC,再 以CD 为直径作半圆交 AC 于点E,若边长AB=10,则△CDE 的面积为( )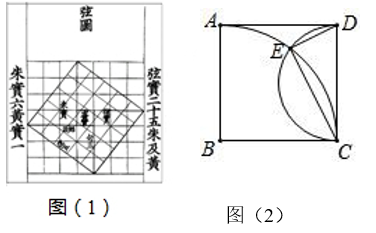 A、20 B、 C、24 D、5. 如图,在平行四边形ABCD中,E为CD延长线上一点,连接BE交AD于F,连接AE,则图中与△DEF相似(不包括本身)的三角形共有( )
A、20 B、 C、24 D、5. 如图,在平行四边形ABCD中,E为CD延长线上一点,连接BE交AD于F,连接AE,则图中与△DEF相似(不包括本身)的三角形共有( ) A、1个 B、2个 C、3个 D、4个6. 如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,设法使斜边保持水平,边与点B在同一直线上.已知直角三角纸板中 , , 测得眼睛D离地面的高度为 , 他与“步云阁”的水平距离为 , 则“步云阁”的高度是( )
A、1个 B、2个 C、3个 D、4个6. 如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,设法使斜边保持水平,边与点B在同一直线上.已知直角三角纸板中 , , 测得眼睛D离地面的高度为 , 他与“步云阁”的水平距离为 , 则“步云阁”的高度是( )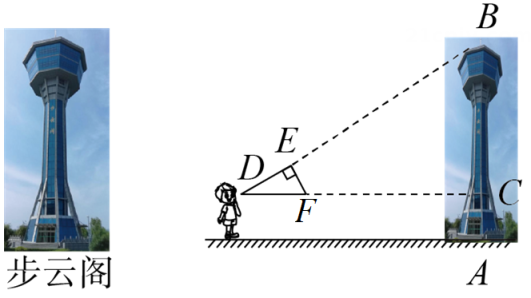 A、 B、 C、 D、7. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( )
A、 B、 C、 D、7. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )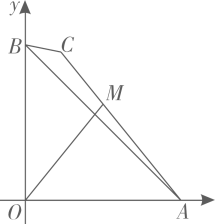 A、( , ) B、( , ) C、( , ) D、( , )9. 如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A、( , ) B、( , ) C、( , ) D、( , )9. 如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到两个矩形都与原矩形相似,则原矩形长与宽的比是( ) A、2:1 B、3:1 C、3:2 D、10. 如图,在平面直角坐标系中,将以原点O为位似中心放大后得到 , 若 , , 则与的面积的比是( )
A、2:1 B、3:1 C、3:2 D、10. 如图,在平面直角坐标系中,将以原点O为位似中心放大后得到 , 若 , , 则与的面积的比是( ) A、1:2 B、1:3 C、1:9 D、9:1
A、1:2 B、1:3 C、1:9 D、9:1二、填空题(每空3分,共18分)
-
11. 四条线段a、b、c、d成比例,满足 , 其中m,m,m,则a=m.12. 如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
 13. 如图,由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形 , 连接和 . 现随机向正方形内掷一枚小针,则针尖落在阴影区域的概率为 .
13. 如图,由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形 , 连接和 . 现随机向正方形内掷一枚小针,则针尖落在阴影区域的概率为 . 14. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么,当t为何值时,以点Q、A、P为顶点的三角形与ABC相似? .15. 如图,矩形的边平行于轴,反比例函数的图象经过点 , 对角线的延长线经过原点 , 且 , 若矩形的面积是8,则的值为 .
14. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么,当t为何值时,以点Q、A、P为顶点的三角形与ABC相似? .15. 如图,矩形的边平行于轴,反比例函数的图象经过点 , 对角线的延长线经过原点 , 且 , 若矩形的面积是8,则的值为 . 16. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.
16. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.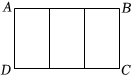
三、作图题(共9分)
-
17. 已知O是坐标原点,的坐标分别为.
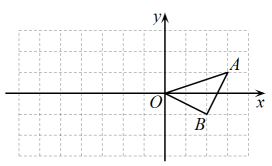
⑴画出绕点O顺时针旋转后得到的 , 并写出的坐标为 ▲ ;
⑵在y轴的左侧以O为位似中心作的位似图形 , 使新图与原图相似比为;
⑶若点在线段上,直接写出变化(2)后点D的对应点的坐标为 ▲ .四、解答题(共9题,共73分)
-
18. 如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.
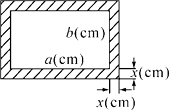 (1)、试用含a,b,x的代数式表示新矩形的长和宽;
(1)、试用含a,b,x的代数式表示新矩形的长和宽;
(2)、试判断原矩形的长、宽与新矩形的长、宽是不是比例线段,并说明理由.
19. 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥AB. (1)、若点D是边BC的中点,且BE=CF,求证:DE=DF;(2)、若AD⊥BC于D,且BD=CD,求证:四边形AEDF是菱形;(3)、若AE=AF=1,求的值.20. 已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)、若点D是边BC的中点,且BE=CF,求证:DE=DF;(2)、若AD⊥BC于D,且BD=CD,求证:四边形AEDF是菱形;(3)、若AE=AF=1,求的值.20. 已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H. (1)、求证:△BEC∽△BCH;(2)、如果BE2=AB·AE,求证:AG=DF.21. 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EC,GD.
(1)、求证:△BEC∽△BCH;(2)、如果BE2=AB·AE,求证:AG=DF.21. 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EC,GD.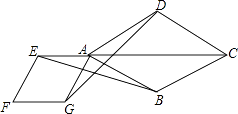 (1)、求证:EB=GD;(2)、若∠DAB=60°,AB=2,AG= ,求GD的长.22. 抛物线交轴于两点(在的左边),交轴于点 .
(1)、求证:EB=GD;(2)、若∠DAB=60°,AB=2,AG= ,求GD的长.22. 抛物线交轴于两点(在的左边),交轴于点 .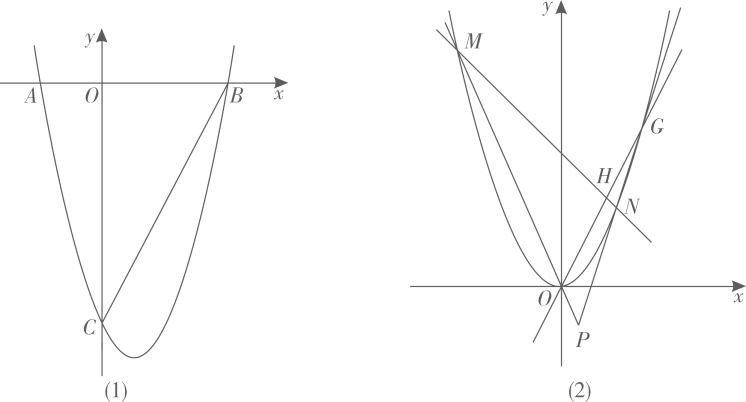 (1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.23. 在四边形ABCD中,对角线AC、BD交于点O,若四边形ABCD是正方形,如图1:则有AC=BD,AC⊥BD.
(1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.23. 在四边形ABCD中,对角线AC、BD交于点O,若四边形ABCD是正方形,如图1:则有AC=BD,AC⊥BD.
旋转图1中的Rt△COD到图2所示的位置,AC’与BD’有什么关系?(直接写出);
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC’与BD’又有什么关系?写出结论并证明.
24. 【探究证明】(1)、某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: = ;
【结论应用】
 (2)、如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 = ,则 的值为;
(2)、如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 = ,则 的值为;【联系拓展】
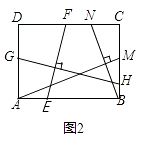 (3)、如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
(3)、如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.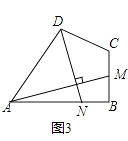 25. 【问题呈现】
25. 【问题呈现】和都是直角三角形, , 连接 , , 探究 , 的位置关系.
 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
26. 综合与实践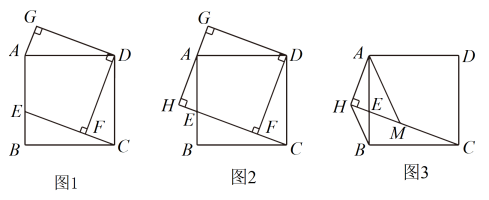 (1)、【思考尝试】
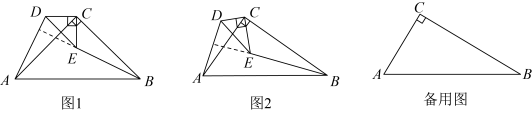
(1)、【思考尝试】数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,于点F, , , . 试猜想四边形的形状,并说明理由;
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边上一点,于点F,于点H,交于点G,可以用等式表示线段 , , 的数量关系,请你思考并解答这个问题;
(3)、【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边上一点,于点H,点M在上,且 , 连接 , , 可以用等式表示线段 , 的数量关系,请你思考并解答这个问题.
-