2023年浙教版数学九年级上册第四章 相似三角形 章末检测(B卷)
试卷更新日期:2023-08-20 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如果 , 那么下列比例式中正确的是( )A、 B、 C、 D、2. 下列各组中的四条线段是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,3. 如图,l1 , l2 , l3 , l4是一组平行线,l5 , l6与这组平行线依次相交于点A,B,C,D和E,F,G,H.若AB∶BC∶CD=2∶3∶4,EG=10,则EH的长为( )
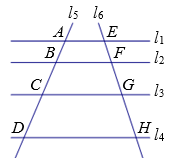 A、14 B、16 C、18 D、204. 的三边长分别为2,3,4,另有一个与它相似的三角形 , 其最长边为16,则的周长是( )A、54 B、36 C、27 D、215. 两个相似三角形的对应边上的中线比为 , 则它们面积比的为( )A、 B、 C、 D、6. 如图示,已知 , 那么添加下列一个条件后,仍无法判定的是( )
A、14 B、16 C、18 D、204. 的三边长分别为2,3,4,另有一个与它相似的三角形 , 其最长边为16,则的周长是( )A、54 B、36 C、27 D、215. 两个相似三角形的对应边上的中线比为 , 则它们面积比的为( )A、 B、 C、 D、6. 如图示,已知 , 那么添加下列一个条件后,仍无法判定的是( )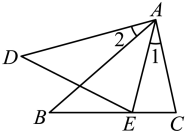 A、 B、 C、 D、7. 如图,为的重心,过点作交于点 , 交于点 , 若 , 则四边形的面积为( )
A、 B、 C、 D、7. 如图,为的重心,过点作交于点 , 交于点 , 若 , 则四边形的面积为( ) A、 B、1.5 C、2 D、38. 国旗法规定:所有国旗均为相似矩形,在下列四面国旗中,其中只有一面不符合标准,这面国旗是( )A、
A、 B、1.5 C、2 D、38. 国旗法规定:所有国旗均为相似矩形,在下列四面国旗中,其中只有一面不符合标准,这面国旗是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
9. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )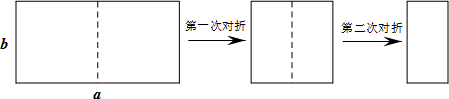 A、a= b B、a=2b C、a=2 b D、a=4b10. 下列三个关于位似图形的表述:
A、a= b B、a=2b C、a=2 b D、a=4b10. 下列三个关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
其中正确命题的序号是( )
A、①② B、②③ C、①③ D、①②③二、填空题(每空4分,共24分)
-
11. 若线段AB=10,且点C是AB的黄金分割点,且BC>AC,则BC的长为 .12. 如图,在ΔABC中,BC=20,点B1 , B2 , B3 , B4和点C1 , C2 , C3 , C4分别是AB,AC的5等分点,则B1C1+B2C2+B3C3+B4C4的值为。
 13. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为.
13. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为. 14. 如图,在中,.点P从点C出发,以的速沿着向点A匀速运动,同时点Q从点B出发,以的速度沿向点C匀速运动,当一个点到终点时,另一个点随之停止.经过秒后,与相似.
14. 如图,在中,.点P从点C出发,以的速沿着向点A匀速运动,同时点Q从点B出发,以的速度沿向点C匀速运动,当一个点到终点时,另一个点随之停止.经过秒后,与相似. 15.
15.在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A1B1C1 , 使△A1B1C1与格点三角形ABC相似(相似比不为1).
.
 16. 如图,矩形的对角线 , 相交于点 , 过点作 , 交于点 , 若 , , 则的长为.
16. 如图,矩形的对角线 , 相交于点 , 过点作 , 交于点 , 若 , , 则的长为.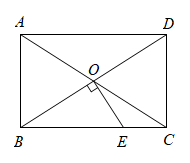
三、作图题(共9分)
-
17. 如图,△ABC中,A(-4,4),B(-4,-2),C(-2,2).

①请画出将△ABC向右平移8个单位长度后的△A1BlC1;
②以O为位似中心,将△A1BlC1缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2.
③画出一个三角形,使它与△ABC相似,且相似比是无理数,并写出所画三角形与△ABC的相似比.
四、解答题(共8题,共57分)
-
18. 已知 .(1)、若 , 求 , 的值;(2)、若 , 求的值.19. 如图,在矩形中,点E,F分别在边 , 上, , , , , , 求的长.
 20. 一个矩形ABCD的较短边长为2.
20. 一个矩形ABCD的较短边长为2.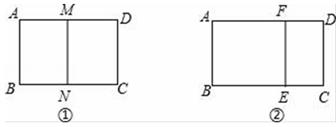 (1)、如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;(2)、如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.21. 如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.
(1)、如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;(2)、如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.21. 如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F. (1)、求证:DE=EF;(2)、连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.22. 如图,在等腰三角形中, , 点是的中点,点 , 分别在线段 , 上,连结 , 交于点 , .
(1)、求证:DE=EF;(2)、连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.22. 如图,在等腰三角形中, , 点是的中点,点 , 分别在线段 , 上,连结 , 交于点 , . (1)、求证:;(2)、若 , , 求的值.23. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .
(1)、求证:;(2)、若 , , 求的值.23. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .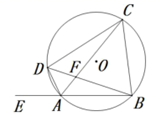 (1)、求证: 平分 ;(2)、若 ,求证: .24. 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)、求证: 平分 ;(2)、若 ,求证: .24. 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离. 25. 如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.
25. 如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.
 (1)、如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是;(2)、如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;(3)、如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”,请写出AD长度的所有可能值.
(1)、如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是;(2)、如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;(3)、如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”,请写出AD长度的所有可能值.
-