2023年浙教版数学九年级上册4.7图形的位似同步测试（培优版）

试卷更新日期：2023-08-20 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，在4×7的方格中，点A，B， C， D在格点上，线段CD是由线段AB位似放大得到，则它们的位似中心是（）

A、点P₁ B、点P₂ C、点P₃ D、点P₄

查看试题解析
2. 如图，在平面直角坐标系中，已知点 $A (- 2 ， 1)$ ， $B (- 1 ， 2)$ ，以原点 $O$ 为位似中心，相似比为2，把 $△ A B O$ 放大，则点 $B$ 的对应点 $B^{'}$ 的坐标是（）

A、 $(- 4 ， 2)$ B、 $(- 2 ， 4)$ C、 $(- 4 ， 2)$ 或 $(- 2 ， 4)$ D、 $(- 2 ， 4)$ 或 $(2 ， - 4)$

查看试题解析
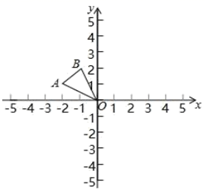3. 在如图所示的网格中，以点O为位似中心，四边形 $A B C D$ 的位似图形是（）

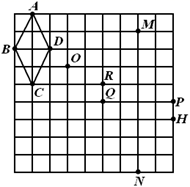A、四边形 $N P M Q$ B、四边形 $N P M R$ C、四边形 $N H M Q$ D、四边形 $N H M R$

查看试题解析
4. 如图，点 $A (0 ， 4)$ ， $B (3 ， 4)$ ，以原点O为位似中心，把线段AB缩短为原来的一半，得到线段CD，其中点C与点A对应，点D与点B对应，则点D的横坐标为（）

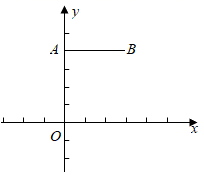A、2 B、2或-2 C、 $\frac{3}{2}$ D、 $\frac{3}{2}$ 或- $\frac{3}{2}$

查看试题解析
5. 在方格图中，以格点为顶点的三角形叫做格点三角形．在如图所示的平面直角坐标系中，格点 $△ A B C 、 △ D E F$ 成位似关系，则位似中心的坐标为（）

A、 $(- 1 ， 0)$ B、 $(0 ， 0)$ C、 $(0 ， 1)$ D、 $(1 ， 0)$

查看试题解析
6. 如图， $△ A B C$ 与 $△ D E F$ 位似，位似中心为点 $O$ .若 $△ A B C$ 的周长与 $△ D E F$ 的周长比为 $\frac{4}{9}$ ，则 $A O ： D O$ 的值为（）

A、 $2 ： 3$ B、 $2 ： 5$ C、 $4 ： 5$ D、 $4 ： 9$

查看试题解析
7. 如图，△AOC中三个顶点的坐标分别为（4，0）、（0，0）、（4，3），AP为△AOC中线，以O为位似中心，把△AOP每条边扩大到原来的2倍，得到 $△ A^{'} O P^{'}$ ，则 $P P^{'}$ 的长为（）

A、 $\frac{5}{4}$ B、 $\frac{5}{2}$ C、 $\frac{5}{4}$ 或 $\frac{15}{4}$ D、 $\frac{5}{2}$ 或 $\frac{15}{2}$

查看试题解析
8. 下列说法正确的是（）

A、若点C是线段AB的黄金分割点，AB=2，则AC= $\sqrt{5} - 1$ B、平面内，经过矩形对角线交点的直线，一定能平分它的面积 C、两个正六边形一定位似 D、菱形的两条对角线互相垂直且相等

查看试题解析
9. 如图，正方形 $O E F G$ 和正方形 $A B C D$ 是位似图形，且点D与点G是一对对应点，点 $D (2 ， 2)$ ，点 $G (0 ， 1)$ ，则它们位似中心的坐标是（）

A、 $(- 2 ， 0)$ B、 $(- 1 ， 0)$ C、 $(0 ， 0)$ D、 $(- 3 ， 0)$

查看试题解析
10. 在平面直角坐标系中， $△ O A B$ 各顶点的坐标分别为： $O (0 ， 0) ， A (1 ， 2) ， B (0 ， 3)$ ，以O为位似中心， $△ O A^{'} B^{'}$ 与 $△ O A B$ 位似，若B点的对应点 $B ′$ 的坐标为 $(0 ， - 9)$ ，则A点的对应点 $A ′$ 坐标为（）

A、 $(3 ， 6)$ B、 $(- 3 ， - 6)$ C、 $(3 ， - 6)$ D、 $(- 3 ， - 6)$

查看试题解析

二、填空题（每空4分，共24分）

11. 如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的 $\frac{1}{2}$ ，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为．

查看试题解析
12. 如图是三角尺在灯泡O的照射下在墙上形成的影子．现测得 $O A = 20 c m$ ， $O A^{'} = 50 c m$ ，则这个三角尺的周长与它在墙上形成的影子的周长之比是．

查看试题解析
13. 如图，在平面直角坐标系中，四边形 $O A B C$ 的顶点坐标分别是 $O (0 ， 0) ， A (1 ， 0) ， B (2 ， 3) ， C (- 1 ， 2)$ ，若四边形 $O A^{'} B^{'} C^{'}$ 与四边形 $O A B C$ 关于原点 $O$ 位似，且四边形 $O A^{'} B^{'} C^{'}$ 的面积是四边形 $O A B C$ 面积的4倍，则第一象限内点 $B^{'}$ 的坐标为．

查看试题解析
14. 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1∶2，∠OCD=90°，CO=CD=2，则点B的坐标为．

查看试题解析
15. 如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A、B、D在x轴上，若等边△BDE的边长为6，则点C的坐标为．

查看试题解析
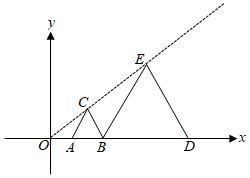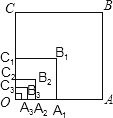
16.
如图，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变化后得正方形OA₁B₁C₁ ，其边长OA₁缩小为OA的 $\frac{1}{2}$ ，经第二次变化后得正方形OA₂B₂C₂ ，其边长OA₂缩小为OA₁的 $\frac{1}{2}$ ，经第，三次变化后得正方形OA₃B₃C₃ ，其边长OA₃缩小为OA₂的 $\frac{1}{2}$ ， …，依次规律，经第n次变化后，所得正方形OA_nB_nC_n的边长为正方形OABC边长的倒数，则n= ．

查看试题解析

三、解答题（共8题，共66分）

17. 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为 $O (0 ， 0)$ ， $A (4 ， 0)$ ， $B (6 ， 4)$ ， $C (0 ， 6)$ ，将其顶点的坐标缩小为原来的 $\frac{1}{2}$ ，画出得到的四边形 $O A^{'} B^{'} C^{'}$ .并判断这两个四边形是位似图形吗？若是，四边形 $O A^{'} B^{'} C^{'}$ 与四边形 $O A B C$ 的相似比是多少？

查看试题解析
18. 在平面直角坐标系中，抛物线L：y＝﹣x²+x+2与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）.

(1)、求A、B、C三点的坐标；

(2)、连接AC、BC，以点C为位似中心，将△ABC扩大到原来的2倍得到△A₁B₁C，其中点A₁、B₁分别是点A、B的对应点，如何平移抛物线L才能使其同时经过点A₁、B₁ ，求出所有的平移方式.

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 1)$ 、 $B (- 3 ， 2)$ 、 $C (- 1 ， 4)$

(1)、以原点O为位似中心，在第二象限内画出将 $△ A B C$ 放大为原来的2倍后的 $△ A_{1} B_{1} C_{1}$ ．

(2)、画出 $△ A B C$ 绕O点顺时针旋转 $90 °$ 后得到的 $△ A_{2} B_{2} C_{2}$ ．

(3)、直接写出点B所经过的路径长．

查看试题解析
20. 已知：在平面直角坐标系内， $△ A B C$ 三个顶点的坐标分别为 $A (0 ， 3)$ 、 $B (3 ， 4)$ 、 $C (2 ， 2) ($ 正方形网格中每个小正方形的边长均是1个单位长度 $)$ ．

⑴画出 $△ A B C$ 向下平移4个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ，点 $C_{1}$ 的坐标是 ▲ $；$

⑵以点 $B$ 为位似中心，在网格中画出 $△ A_{2} B_{2} C_{2}$ ，使 $△ A_{2} B_{2} C_{2}$ 与 $△ A B C$ 位似，且位似比为 $2 ： 1$ ，点 $C_{2}$ 的坐标是 ▲ $；$

⑶求 $△ A_{2} B_{2} C_{2}$ 的面积．

查看试题解析
21. 如图，在直角坐标系中，边长为1的小正方形组成的网格中，给出了格点△ABC（顶点为网格线的交点），在给定的网格中，解答下列问题：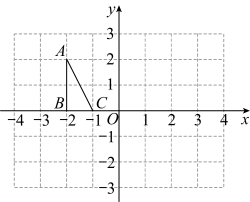
⑴以A为位似中心，将△ABC按相似比2：1放大，得到△AB₁C₁ ，画出△AB₁C₁.
⑵以C₁为旋转中心，将△AB₁C₁顺时针旋转90°，得到△A₁B₂C₁.
①画出△A₁B₂C₁；
②求点A的运动路径长.

查看试题解析
22. 放缩尺是一种绘图工具，它能把图形放大或缩小．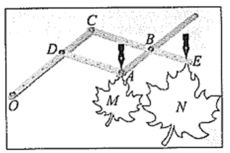
制作：把钻有若干等距小孔的四根直尺用螺栓分别在点A，B，C，D处连接起来，使得直尺可以绕着这些点转动，O为固定点， $O D = D A = C B$ ， $D C = A B = B E$ ，在点A，E处分别装上画笔．
画图：现有一图形M，画图时固定点O，控制点A处的笔尖沿图形M的轮廓线移动，此时点E处的画笔便画出了将图形M放大后的图形N．
原理：
连接 $O A$ ， $O E$ ，可证得以下结论：
① $△ O D A$ 和 $△ O C E$ 为等腰三角形，则 $∠ D O A = \frac{1}{2} (180 ° - ∠ O D A)$ ， $∠ C O E = \frac{1}{2}$ （180°-∠            ▲             ）；
②四边形 $A B C D$ 为平行四边形（理由是            ▲            ）；
③ $∠ D O A = ∠ C O E$ ，于是可得O，A，E三点在一条直线上；
④当 $\frac{D C}{C B} = \frac{3}{5}$ 时，图形N是以点O为位似中心，把图形M放大为原来的            ▲            倍得到的．

查看试题解析
23. 阅读与思考
探索位似的性质

利用图形计算器或计算机等信息技术工具，可以很方便地将图形放大或缩小，还可以探索位似的性质．

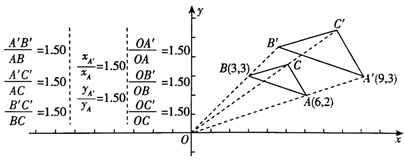
小明利用几何画板软件，尝试用“观察—猜想-验证—应用”的方法进行探究，步骤如下∶如图（1），任意画一个△ABC，以点O为位似中心，自选新旧图形的相似比为k，得到△A´B´C´．

图（1）

第一步，度量对应边的长度，并计算它们的比值，发现结果与k的值相等．

第二步，以0为原点建立平面直角坐标系，分别度量点A，A´的横坐标，并计算比值；分别度量点A，A´的纵坐标，并计算比值，观察比值与k的关系，发现它们相等．接下来对其他顶点进行相同的操作，得出相同的结论．

第三步，作线段 OA，OA´，OB，OB´，OC，OC´，度量它们，发现的结论是：_________．

第四步，任意改变△ABC的位置成形状，发现上面探究得出的结论仍然成立．

于是，小明总结并得出了位似的性质．

任务∶

(1)、第三步发现的结论是：．．

(2)、已知图（1）中A（6，2），A´（9，3），B（3，3），S_△_ABC=2，则点B´的坐标是， S_△_A´B´C´= ．

(3)、如图（2），以点A为位似中心，画出与矩形 ABCD的相似比为0.75的一个图形．

查看试题解析
24.

(1)、发现探究：如图1，矩形 $A B C D$ 和矩形 $A E F G$ 位似， $A B ： B C = \sqrt{3} ： 1$ ，连接 $A C$ ，则线段 $B E$ 与 $C F$ 有何数量关系，关系是.直线 $B E$ 与直线 $C F$ 所夹锐角的度数是.

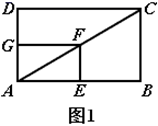(2)、拓展探究：如图2，将矩形 $A E F G$ 绕点 $A$ 逆时针旋转角 $α$ $(0 ° < α < 360 °)$ ，上面的结论是否仍然成立？如果成立，请就图2给出的情况加以证明.

(3)、问题解决：若点 $M$ 是 $C F$ 的中点， $A F = \frac{1}{2} A C$ ，连接 $G M$ ， $B C = 4 \sqrt{3}$ ，在矩形 $A E F G$ 绕点 $A$ 旋转过程中，请直接写出 $G M$ 长的取值范围.

查看试题解析

2023年浙教版数学九年级上册4.7图形的位似 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学九年级上册4.7图形的位似同步测试（培优版）