2023年浙教版数学九年级上册4.6相似多边形 同步测试（提升版）
试卷更新日期：2023-08-20 类型：同步测试
一、选择题（每题4分，共40分）
-
1. 下列语句中，正确的有（ ）
①相等的圆心角所对的弧相等；
②等弦对等弧；
③若两个相似多边形的面积比为16：9，那么这两个相似多边形的周长比是4：3；
④已知线段AB＝2，点C是AB的黄全分割点，则；
⑤三角形的外心到三角形的三边距离相等.
A、1个 B、2个 C、3个 D、4个2. 下列与相似有关的命题中，正确的是（ ）①所有的等腰三角形都相似；②所有的矩形都相似；③所有的正六边形都相似.
A、①②③ B、① C、② D、③3. 如图，矩形ABCD的对称轴分别交AB于点E，交CD于点F．若矩形AEFD与矩形ABCD相似，则AB：BC的值为（ ）
A、2 B、 C、 D、4. 若一个矩形剪掉一个面积最大的正方形，剩下的小矩形与原来的矩形相似，且原矩形的较长边长为 ， 则剩下的小矩形的较短边长为（ ）A、 B、 C、 D、5. 如图，在四边形ABCD中，∠A＝∠B＝90°，点F为边CD上一点，且FE⊥AB交AB于点E，若AD＝2，BC＝8，四边形AEFD～四边形EBCF，则的值是（ ）
A、 B、 C、 D、6. 如果两个相似多边形的周长比是2：3，那么它们的面积比为（ ）A、2：3 B、4：9 C、： D、16：817. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（ ）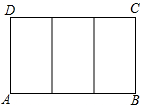
A、 B、 C、2 D、8. 如图2中的矩形边长分别是将图1中的矩形边长4拉长2x，边长5拉长x得到的，若两个矩形相似（不全等），则x的值是（ ）
A、3 B、4 C、5 D、69. 若矩形ABCD∽矩形EFGH，相似比为2∶3，已知AB＝3 cm，BC＝5 cm，则矩形EFGH的周长是（ ）A、16 cm B、12 cm C、24 cm D、36 cm10. 在平面直角坐标系中，已知矩形与矩形关于坐标原点O位似，且矩形的面积等于矩形面积的4倍，若矩形的顶点B的坐标为 ， 则B的对应点的坐标为（ ）A、 B、或 C、 D、或二、填空题（每空5分，共30分）
-
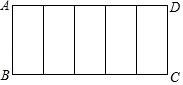
11. 如图，矩形 被分割为5个全等的长方形，若这5个矩形都与矩形 相似，则 的值是.
12. 如果四边形ABCD的四条边长分别为54cm、48cm、45cm、63cm，另一个和它相似的四边形的最长边长为21cm，那么这个四边形的最短边的长度为.13. 如图，将一张矩形纸片沿折叠，得到两个全等的小矩形.如果矩形矩形 ， 那么的值是.
14. 两个相似多边形的周长比是3：4，其中较小的多边形的面积为 ， 则较大的多边形的面积为cm2 ．15. 与相似，的对应边的面积为10．则的面积是 ．16. 如图所示，一般书本的纸张是原纸张多次对开得到，矩形 沿 对开后，再把矩形 沿 对开，依次类推，若各种开本的矩形都相似，那么 的值为 ．
三、解答题（共5题，共50分）
-
17. 如图，点 是菱形 对角线 的延长线上任意一点，以线段 为边作一个菱形 ，且菱形 菱形 ，连接 ，求证： .
18. 学生会要举办一个校园书画艺术展览会，为国庆献礼，小华和小刚准备将长AD为400cm，宽AB为130cm的矩形作品四周镶上彩色纸边装饰，如图所示，两人在设计时要求内外两个矩形相似，矩形作品面积是总面积的 ，他们一致认为上下彩色纸边要等宽，左右彩色纸边要等宽，这样效果最好，请你帮助他们设计彩色纸边宽度.
19. 如图，把一个矩形剪去一个边长和它的宽相等的正方形，若剩下的矩形与原矩形相似．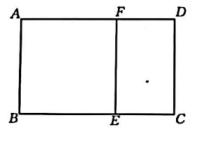
(1)、求原矩形的长和宽的比．(2)、若 ， 求矩形的面积．20. 阅读理解：给定一个矩形，如果存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的一半，则这个矩形是给定矩形的“减半”矩形.如图，矩形 是矩形ABCD的“减半”矩形.请你解决下列问题：
(1)、当矩形的长和宽分别为9，1时，它是否存在“减半”矩形？请作出判断，如果不存在，请说明理由；如果存在，请求出“减半”矩形的长宽.(2)、边长为a的正方形存在“减半”正方形吗？如果存在，求出“减半”正方形的边长；如果不存在，请说明理由.21. 如图，四边形ABCD为平行四边形，AE平分∠BAD交BC于点E，过点E作EF∥AB，交AD于点F，连接BF．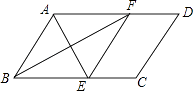
(1)、求证：BF平分∠ABC；(2)、若AB=6，且四边形ABCD∽四边形CEFD，求BC长．