2023年浙教版数学九年级上册4.6相似多边形 同步测试(基础版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 两个相似六边形,若对应边之比为3:2,则这两个六边形的周长比为( )A、9:4 B、9:2 C、3:1 D、3:22. 已知四边形ABCD∽四边形EFGH,且AB=3,EF=4,FG=5.则四边形EFGH与四边形ABCD的相似比为( )A、3:4 B、3:5 C、4:3 D、5:33. 如图,矩形ABCD∽矩形EFGH,已知 , , , 则FG的长为( )
 A、8cm B、10cm C、12cm D、15cm4. 如图,已知四边形四边形 , , , 则的长是( ).
A、8cm B、10cm C、12cm D、15cm4. 如图,已知四边形四边形 , , , 则的长是( ).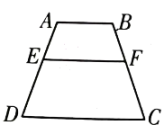 A、6 B、 C、 D、45. 如图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
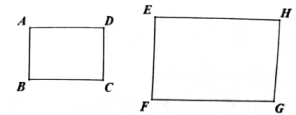
A、6 B、 C、 D、45. 如图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )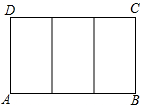 A、 B、 C、2 D、6. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、7. 如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B等于( )
A、 B、 C、2 D、6. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、7. 如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B等于( )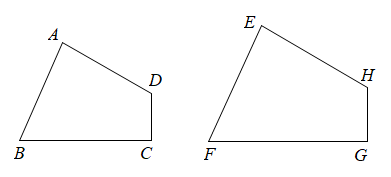 A、55° B、65° C、75° D、85°8. 如图所示,已知矩形的边长为8cm,边长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( )
A、55° B、65° C、75° D、85°8. 如图所示,已知矩形的边长为8cm,边长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( ) A、21cm2 B、24cm2 C、27cm2 D、30cm29. 一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为 , 则它的最大边长为( )A、 B、 C、 D、10. 两个相似多边形的相似比是3:4,其中小多边形的面积为18cm2 , 则较大多边形的面积为( )A、16cm2 B、54cm2 C、32cm2 D、48cm2
A、21cm2 B、24cm2 C、27cm2 D、30cm29. 一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为 , 则它的最大边长为( )A、 B、 C、 D、10. 两个相似多边形的相似比是3:4,其中小多边形的面积为18cm2 , 则较大多边形的面积为( )A、16cm2 B、54cm2 C、32cm2 D、48cm2二、填空题(每空4分,共24分)
-
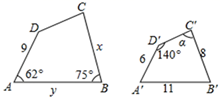
11. 若两个相似多边形的相似比是2:3,则它们的周长比是 .12. 图中的两个四边形相似,则.
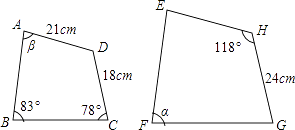
 13. 如图,四边形四边形 , 若 , , , 则°.
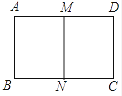
13. 如图,四边形四边形 , 若 , , , 则°.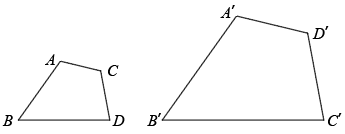 14. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是元.15. 如图,矩形中, , 剪去一个矩形后,余下的矩形矩形 , 则的长为 .
14. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是元.15. 如图,矩形中, , 剪去一个矩形后,余下的矩形矩形 , 则的长为 . 16. 四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与点A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是.
16. 四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与点A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是.三、解答题(共7题,共66分)
-
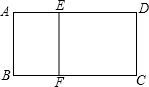
17. 两个相似多边形的最长边分别为6cm和8cm,它们的周长之和为56cm,面积之差为28cm2 , 求较小相似多边形的周长与面积.18. 如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
 19. 如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
19. 如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.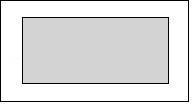 20. 在一块长和宽分别为3m和2m的矩形塑料板四周镶上木条.若在长边上镶上的木条的宽为0.5m.则要使木条内缘围成的矩形与木条外缘围成的矩形相似,在宽边上镶的木条的宽应是多少?
20. 在一块长和宽分别为3m和2m的矩形塑料板四周镶上木条.若在长边上镶上的木条的宽为0.5m.则要使木条内缘围成的矩形与木条外缘围成的矩形相似,在宽边上镶的木条的宽应是多少?