2023年浙教版数学九年级上册4.5相似三角形的性质与应用 同步测试(提升版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题 (每题3分,共30分)
-
1. 已知△ABC∽△A'B'C,AD和A'D'是它们的对应高线,若AD=4,A'D'=1,则△ABC与△A'B'C的面积比是( )A、16:1 B、4:1 C、4:3 D、4:92. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BD交于点F,则S△DEF:S△ADF:S△ABF等于( )
 A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:253. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( )
A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:253. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( ) A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )
A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )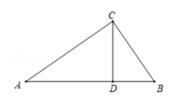 A、4 B、6 C、2 D、35. 如图,点G是的重心,于点H,若 , , 则△ABC的面积为( )
A、4 B、6 C、2 D、35. 如图,点G是的重心,于点H,若 , , 则△ABC的面积为( ) A、2 B、3 C、4 D、66. 如图,在直角坐标系中,已知点 , 将沿着轴正方向平移,使点平移至原点 , 得到交于点 , 则的长为( )
A、2 B、3 C、4 D、66. 如图,在直角坐标系中,已知点 , 将沿着轴正方向平移,使点平移至原点 , 得到交于点 , 则的长为( ) A、 B、 C、 D、17. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( )
A、 B、 C、 D、17. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( ) A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S48. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( )
A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S48. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( ) A、的面积 B、的面积 C、的面积 D、的面积9. 如图,线段AB,EF,CD分别表示人,竹竿,楼房的高度,且A,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是( )
A、的面积 B、的面积 C、的面积 D、的面积9. 如图,线段AB,EF,CD分别表示人,竹竿,楼房的高度,且A,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是( ) A、25m B、26.5m C、50m D、51.5m10. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( )
A、25m B、26.5m C、50m D、51.5m10. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( ) A、1cm B、cm C、2cm D、cm
A、1cm B、cm C、2cm D、cm二、填空题(每题4分,共24分)
-
11. 如果两个相似三角形的面积比为4:9,较小三角形的周长为4,那么这两个三角形的周长和为.12. 如图所示的正方形网格中,每个小正方形的边长均为1,A、B、C、E、F均在格点上.若△ABC∽△DFE,则△DFE的面积是 .
 13. 在相似的两个三角形中,已知其中一个三角形三边的长是3,4,5,另一个三角形有一边长是2,则另一个三角形的周长是.14. 三角形三边长为5,5,6,则这个三角形的外心和重心的距离为.15. 为了测量河宽AB,有如下方法:如图,取一根标尺CD横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=15米,OC=10米,AC=20米,则河宽AB的长度为米.
13. 在相似的两个三角形中,已知其中一个三角形三边的长是3,4,5,另一个三角形有一边长是2,则另一个三角形的周长是.14. 三角形三边长为5,5,6,则这个三角形的外心和重心的距离为.15. 为了测量河宽AB,有如下方法:如图,取一根标尺CD横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=15米,OC=10米,AC=20米,则河宽AB的长度为米. 16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可.
16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可. (1)、 km.(2)、 = .
(1)、 km.(2)、 = .三、解答题(共8题,共66分)
-
17. 如图,在 中,D,E分别是AB,AC上的点, 平分 交DE于点 ,交BC于点 .
 (1)、求证: .(2)、若点 是 的重心, ,求AB的长.18. 如图,是的外接圆, , 于点D,的延长线分别交于点E、F.
(1)、求证: .(2)、若点 是 的重心, ,求AB的长.18. 如图,是的外接圆, , 于点D,的延长线分别交于点E、F. (1)、求证:.(2)、若 , , 求AC的长.19. 如图,内接于 , , 的外角的平分线交于点D,连接 , , 交于点F.
(1)、求证:.(2)、若 , , 求AC的长.19. 如图,内接于 , , 的外角的平分线交于点D,连接 , , 交于点F. (1)、求证:是等腰三角形.(2)、若.
(1)、求证:是等腰三角形.(2)、若.①求证:.
②若的半径为5, , 求的值.
20. 已知在矩形中, , , 点是边上的一个动点,以为边,在的右侧作矩形 , 且 , 连接 , . (1)、如图1,若 , 点运动到的中点时,求的长.(2)、如图2,判断与有怎样的数量关系,并说明理由.(3)、当点从点运动到点时,请直接写出点的运动路径长.21. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的长度AD为100cm.
(1)、如图1,若 , 点运动到的中点时,求的长.(2)、如图2,判断与有怎样的数量关系,并说明理由.(3)、当点从点运动到点时,请直接写出点的运动路径长.21. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的长度AD为100cm. (1)、视线∠ABD的度数为 .(用含α的式子表示)(2)、当小然到墙壁PM的距离AB=250cm时,求油画顶部点D到墙壁PM的距离.22. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)、视线∠ABD的度数为 .(用含α的式子表示)(2)、当小然到墙壁PM的距离AB=250cm时,求油画顶部点D到墙壁PM的距离.22. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试. (1)、如图1,垂直于地面放置的正方形框架 , 边长为 , 在其上方点P处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为 . 那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?
(1)、如图1,垂直于地面放置的正方形框架 , 边长为 , 在其上方点P处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为 . 那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?

