2023年浙教版数学九年级上册4.5相似三角形的性质与应用 同步测试(培优版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )
A、30厘米、45厘米; B、40厘米、80厘米; C、80厘米、120厘米; D、90厘米、120厘米2. 如图,小红利用小孔成像原理制作了一个成像装置,他在距离纸筒处准备了一支蜡烛,蜡烛长为 , 纸筒的长度为 , 则这支蜡烛所成像的高度为( ) A、 B、 C、 D、3. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形,A、B、C的纸片的面积分别为S1、S2、S3 , (S1与S2 , S2与S3的相似比相同),相邻纸片之间互不重叠也无缝隙,若S1>S2>S3 , 则这个矩形的面积一定可以表示为( )
A、 B、 C、 D、3. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形,A、B、C的纸片的面积分别为S1、S2、S3 , (S1与S2 , S2与S3的相似比相同),相邻纸片之间互不重叠也无缝隙,若S1>S2>S3 , 则这个矩形的面积一定可以表示为( )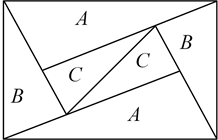 A、4S1 B、6S2 C、4S2+3S3 D、3S1+4S34. 如图,在矩形 中, , 分别为 , 的中点,线段 , 与对角线 分别交于点 .设矩形 的面积为 ,则下列结论错误的是( )
A、4S1 B、6S2 C、4S2+3S3 D、3S1+4S34. 如图,在矩形 中, , 分别为 , 的中点,线段 , 与对角线 分别交于点 .设矩形 的面积为 ,则下列结论错误的是( ) A、 B、 C、 D、5. 如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合), , 分别表示四边形和的面积,则的最大值是( )
A、 B、 C、 D、5. 如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合), , 分别表示四边形和的面积,则的最大值是( )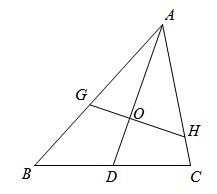 A、 B、1 C、 D、6. 如图,H是△ABC的重心,延长AH交BC于D,延长BH交AC于M,E是DC上一点,且DE∶EC=5∶2,连结AE交BM于G,则BH∶HG∶GM等于( )
A、 B、1 C、 D、6. 如图,H是△ABC的重心,延长AH交BC于D,延长BH交AC于M,E是DC上一点,且DE∶EC=5∶2,连结AE交BM于G,则BH∶HG∶GM等于( ) A、7∶5∶2 B、13∶5∶2 C、5∶3∶1 D、26∶10∶37. 如图, , , , 分别是矩形四条边上的点,连接 , 相交于点 , 且 , , 矩形矩形 , 连接交 , 于点 , , 下列一定能求出面积的条件是( )
A、7∶5∶2 B、13∶5∶2 C、5∶3∶1 D、26∶10∶37. 如图, , , , 分别是矩形四条边上的点,连接 , 相交于点 , 且 , , 矩形矩形 , 连接交 , 于点 , , 下列一定能求出面积的条件是( ) A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差8. 如图,在矩形中,过点作对角线的垂线并延长,与的延长线交于点 , 与交于点 , 垂足为点 , 连接 , 且 , 则下列结论正确的有( )个:①;②;③;④
A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差8. 如图,在矩形中,过点作对角线的垂线并延长,与的延长线交于点 , 与交于点 , 垂足为点 , 连接 , 且 , 则下列结论正确的有( )个:①;②;③;④ A、1 B、2 C、3 D、49. 如图,在正方形ABCD中,点E是边BC上一点,且 . 过点B作 , 交边CD于点F.以C为圆心,CF长为半径画圆,交边BC于点G,连接DG,交BF于点H.则( )
A、1 B、2 C、3 D、49. 如图,在正方形ABCD中,点E是边BC上一点,且 . 过点B作 , 交边CD于点F.以C为圆心,CF长为半径画圆,交边BC于点G,连接DG,交BF于点H.则( ) A、10:3 B、3:1 C、8:3 D、5:310. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )
A、10:3 B、3:1 C、8:3 D、5:310. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )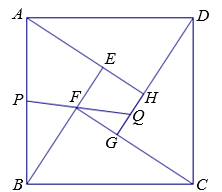 A、 B、3 C、 D、4
A、 B、3 C、 D、4二、填空题(每空3分,共18分)
-
11. 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB=7,则AC=.
 12. 如图,在 中, , ,点D为AC上一点,作 交BC于点E , 点C关于DE的对称点为点O , 以OA为半径作⊙O恰好经过点C , 并交直线DE于点M , N则MN的值为 .
12. 如图,在 中, , ,点D为AC上一点,作 交BC于点E , 点C关于DE的对称点为点O , 以OA为半径作⊙O恰好经过点C , 并交直线DE于点M , N则MN的值为 .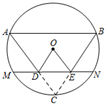 13. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .
13. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .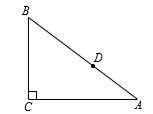 14. 如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则
14. 如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则 15. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是.
15. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是. 16. 某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB上地面,AB=120 cm,Р是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40 cm,斜拉杆AE可绕点A旋转,AE= CP.若∠APE=30°,则BP=cm;伞展开长 PD==300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为cm.
16. 某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB上地面,AB=120 cm,Р是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40 cm,斜拉杆AE可绕点A旋转,AE= CP.若∠APE=30°,则BP=cm;伞展开长 PD==300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为cm.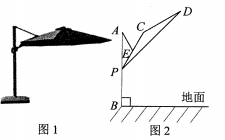
三、解答题(共9题,共72分)
-
17. 如图1,长、宽均为3cm,高为8cm的长方体容器,放置在水平桌面上,里面盛有水,水面高为6cm,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,将这个情景转化成几何图形,如图3所示.
 (1)、利用图1、图2所示水的体积相等,求的长;(2)、求水面高度 .18. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.
(1)、利用图1、图2所示水的体积相等,求的长;(2)、求水面高度 .18. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.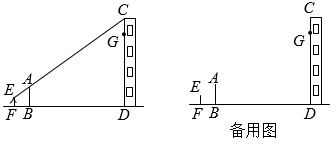 (1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.19. 如图为幸福小区入口处安装的汽车出入道闸示意图.如图1,道闸关闭时,四边形是矩形.如图2,在道闸打开的过程中,边固定,直线l,连杆、分别绕点A、D转动,且边始终与边平行,P为上的一点(不与点C,D重合),过点P作直线l, , 垂足分别为E,F,即四边形是矩形,过点D作 , 垂足为Q,延长与相交于点R.
(1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.19. 如图为幸福小区入口处安装的汽车出入道闸示意图.如图1,道闸关闭时,四边形是矩形.如图2,在道闸打开的过程中,边固定,直线l,连杆、分别绕点A、D转动,且边始终与边平行,P为上的一点(不与点C,D重合),过点P作直线l, , 垂足分别为E,F,即四边形是矩形,过点D作 , 垂足为Q,延长与相交于点R.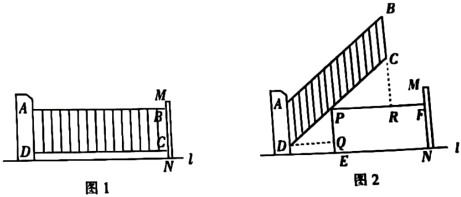 (1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.
(1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.①求点B到地面l的距离;
②求的长.
20. 如图,抛物线经过点、、三点. (1)、求此抛物线的解析式;(2)、P是抛物线上的一个动点,过作轴,垂足为 , 是否存在点 , 使得以、、为顶点的三角形与相似?若存在,请求出符合条件的点的坐标;若不存在,请说明理由;(3)、在直线上方的抛物线是有一点 , 使得的面积最大,求出点的坐标.21. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、求此抛物线的解析式;(2)、P是抛物线上的一个动点,过作轴,垂足为 , 是否存在点 , 使得以、、为顶点的三角形与相似?若存在,请求出符合条件的点的坐标;若不存在,请说明理由;(3)、在直线上方的抛物线是有一点 , 使得的面积最大,求出点的坐标.21. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.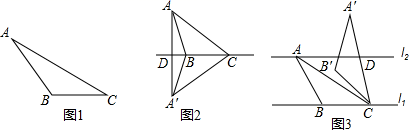 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,DC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形.(填“是”或“否”)
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连接AA'交直线BC于点D.若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2,“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C,A′C所在直线交l2于点D,直接写出CD的值.
22. 在平面直角坐标系中,点O为坐标系的原点,抛物线经过 , 两点,直线与x轴交于点C,与y轴交于点D,点P为直线上的一个动点,连接. (1)、求抛物线的解析式;(2)、如图1,当点P在第一象限时,设点P的横坐标为t,的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,点E在y轴的正半轴上,且 , 连接 , 当直线交x轴正半轴于点L,交y轴于点V时,过点P作交x轴于点G,过点G作y轴的平行线交线段于点F,连接 , 过点G作交线段于点Q,的平分线交x轴于点M,过点M作交于点H,过点H作于点R,若 , 求点P的坐标.23. 如图:
(1)、求抛物线的解析式;(2)、如图1,当点P在第一象限时,设点P的横坐标为t,的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)、如图2,在(2)的条件下,点E在y轴的正半轴上,且 , 连接 , 当直线交x轴正半轴于点L,交y轴于点V时,过点P作交x轴于点G,过点G作y轴的平行线交线段于点F,连接 , 过点G作交线段于点Q,的平分线交x轴于点M,过点M作交于点H,过点H作于点R,若 , 求点P的坐标.23. 如图: (1)、[基础巩固]如图1,在四边形中,对角线平分 , 求证:;(2)、[尝试应用]如图2,四边形为平行四边形,F在边上, , 点E在延长线上,连接、、 , 若 , 求的长;(3)、[拓展提高]如图3,E是内部一点,F为边上一点,连接 , 已知 , , 求的值.24. 如图
(1)、[基础巩固]如图1,在四边形中,对角线平分 , 求证:;(2)、[尝试应用]如图2,四边形为平行四边形,F在边上, , 点E在延长线上,连接、、 , 若 , 求的长;(3)、[拓展提高]如图3,E是内部一点,F为边上一点,连接 , 已知 , , 求的值.24. 如图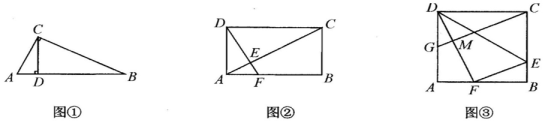 (1)、[基础巩固]如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2 =AD·AB.(2)、[尝试应用] 如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.(3)、[拓展提高] 如图③,在矩形ABCD中,点E在边BC上,NDCE与NDFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.25.(1)、【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:;
(1)、[基础巩固]如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:AC2 =AD·AB.(2)、[尝试应用] 如图②,在矩形ABCD中,AD=2,点F在AB上,FB=2AF,DF⊥AC于点E,求AE的长.(3)、[拓展提高] 如图③,在矩形ABCD中,点E在边BC上,NDCE与NDFE关于直线DE对称,点C的对称点F在边AB上,G为AD中点,连结GC交DF于点M,GC∥FE,若AD=2,求GM的长.25.(1)、【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:; (2)、【尝试应用】
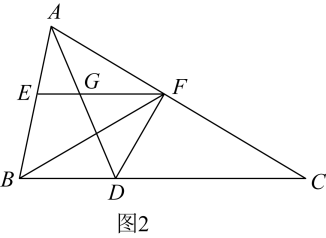
(2)、【尝试应用】如图2,在(1)的条件下,连结 , , 若 , 、恰好将三等分,求的值;
 (3)、【拓展延伸】
(3)、【拓展延伸】如图3,在等边中, , 连结 , 点E在上,若 , 求的值.