2023年浙教版数学九年级上册4.5相似三角形的性质与应用 同步测试(基础版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 两个相似三角形的相似比是4:9,则它们的面积比是( )A、4:9 B、16:81 C、2:3 D、1:32. 已知 , 且.若的周长为8,则的周长是( )A、4 B、8 C、12 D、183. 已知 , 和是它们的对应边上的高,若 , , 则与的面积比是( )A、2:3 B、4:9 C、3:2 D、9:44. 两个相似三角形一组对应角平分线的长分别是2cm和5cm,其中较小三角形的周长是10cm,则较大三角形的周长为( )A、15cm B、18cm C、20cm D、25cm5. 在 中,AD是BC边上的中线,点G是重心,如果 ,那么线段DG的长为( )A、3 B、4 C、9 D、126. 如图,线段 , 相交于点 , , 若 , , , 则的长是( )
 A、3 B、4 C、5 D、67. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )
A、3 B、4 C、5 D、67. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )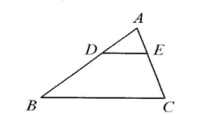 A、 B、 C、 D、8. 如图,在中,点D、E分别在AC、AB上,连接DE,若 , 且 , 则的值为( ).
A、 B、 C、 D、8. 如图,在中,点D、E分别在AC、AB上,连接DE,若 , 且 , 则的值为( ). A、 B、 C、 D、9. 如图,它是物理学中小孔成像的原理示意图,已知物体 , 根据图中尺寸 , 则的长应是( )
A、 B、 C、 D、9. 如图,它是物理学中小孔成像的原理示意图,已知物体 , 根据图中尺寸 , 则的长应是( ) A、15 B、30 C、20 D、1010. 如图,路灯距离地面8米,若身高1.6米的小明在路灯下处测得影子的长为5米,则小明和路灯的距离为( )
A、15 B、30 C、20 D、1010. 如图,路灯距离地面8米,若身高1.6米的小明在路灯下处测得影子的长为5米,则小明和路灯的距离为( ) A、25米 B、15米 C、16米 D、20米
A、25米 B、15米 C、16米 D、20米二、填空题(每空4分,共24分)
-
11. 若 , 它们的面积比为 , 则它们的对应高的比为 .12. 若△ABC∽△A′B′C′,且 , △ABC的周长为12cm,则△A′B′C′的周长为.13. 若△ABC∽△A'B'C',且 , △ABC的周长为12 cm,则△A'B'C'的周长为cm.14. 已知点是的重心,那么15. 如图,在△ABC中,∠AED=∠B,若AB=10,AE=8,DE=6,则BC的长为.
 16. 如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是m.
16. 如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是m.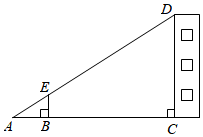
三、解答题(共8题,共66分)
-
17. 如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.
 18. 已知的三边长分别为6,8,10,和相似的的最长边长为30,求的周长.19. 如图,在中,点D在边上, , , , 求的长.
18. 已知的三边长分别为6,8,10,和相似的的最长边长为30,求的周长.19. 如图,在中,点D在边上, , , , 求的长.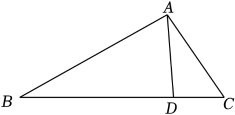 20. 如图,为上一点,若 , , 求证: .
20. 如图,为上一点,若 , , 求证: . 21. 如图,分别是的边 , 上的点, , 若 , 求的值.
21. 如图,分别是的边 , 上的点, , 若 , 求的值.