2023年浙教版数学九年级上册4.3相似三角形 同步测试(培优版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题4分,共40分)
-
1. 已知在△ABC中,AB=6,AC=9,D,E分别是AB,AC边上的点,且AD=2. 若△ABC和△ADE相似,则AE=( )A、5 B、3 C、 D、3或2. 如图,将先向左平移4个单位,得到 , 再以原点O为位似中心,作的位似三角形 , 使它与的相似比为且在同一象限内,则点A的对应点的坐标是( )
 A、 B、 C、 D、3. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( )
A、 B、 C、 D、3. 如图, , 在边上取点P,使得与相似,则满足条件的点P有( ) A、1个 B、2个 C、3个 D、0个4. 如图,内接于 , 且 , 的延长线交于点 , 若与相似,则( ).
A、1个 B、2个 C、3个 D、0个4. 如图,内接于 , 且 , 的延长线交于点 , 若与相似,则( ). A、 B、 C、 D、5. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形.点E是格点四边形ABCD的AB边上一动点,连接ED,EC,若格点 与 相似,则 的长为( )
A、 B、 C、 D、5. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形.点E是格点四边形ABCD的AB边上一动点,连接ED,EC,若格点 与 相似,则 的长为( )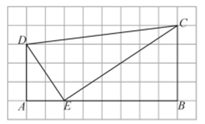 A、 B、 C、 或 D、 或6. 要制作两个形状相同的三角形框架,其中一个三角形的边长分别为8cm,10cm和12cm,另一个三角形的最短边长为2cm,则它的最长边为( )A、3cm B、4cm C、4.5cm D、5cm7. 如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A、 B、 C、 或 D、 或6. 要制作两个形状相同的三角形框架,其中一个三角形的边长分别为8cm,10cm和12cm,另一个三角形的最短边长为2cm,则它的最长边为( )A、3cm B、4cm C、4.5cm D、5cm7. 如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似. A、 B、 C、 或 D、 或8. 如图,在正方形网格中:△ABC、△EDF的顶点都在正方形网格的格点上,△ABC∽△EDF , 则∠ABC+∠ACB的度数为( )
A、 B、 C、 或 D、 或8. 如图,在正方形网格中:△ABC、△EDF的顶点都在正方形网格的格点上,△ABC∽△EDF , 则∠ABC+∠ACB的度数为( ) A、75° B、60° C、55° D、45°9. 如图所示,若甲乙丙丁都是方格纸中的格点.如图,若、、、、、甲、乙、丙、丁都是方格纸中的格点,为使 , 则点应是甲、乙、丙、丁四点中的( )
A、75° B、60° C、55° D、45°9. 如图所示,若甲乙丙丁都是方格纸中的格点.如图,若、、、、、甲、乙、丙、丁都是方格纸中的格点,为使 , 则点应是甲、乙、丙、丁四点中的( ) A、甲 B、乙 C、丙 D、丁10. 如图,已知直角坐标系中四点A(﹣2,4)、B(﹣2,0)、C(2,﹣3)、D(2,0).若点P在x轴上,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,则所有符合上述条件的点P的个数是( )
A、甲 B、乙 C、丙 D、丁10. 如图,已知直角坐标系中四点A(﹣2,4)、B(﹣2,0)、C(2,﹣3)、D(2,0).若点P在x轴上,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,则所有符合上述条件的点P的个数是( ) A、1个 B、2个 C、3 个 D、4个
A、1个 B、2个 C、3 个 D、4个二、填空题(每空6分,共30分)
-
11. 如图,D、E分别是ΔABC的边AB、AC上的动点,若 , 且ΔADE与ΔABC相似,则AD的长度是.
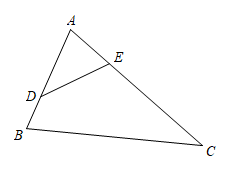 12. 如图,、交于点 , 且 , , , 当时,与相似.
12. 如图,、交于点 , 且 , , , 当时,与相似. 13. 如图,中, , 在的延长线上截取 , 连接 , 过点作于点 , 交于点 , 连接 , 点为射线上一个动点,若 , , 当与相似时,的长为 .
13. 如图,中, , 在的延长线上截取 , 连接 , 过点作于点 , 交于点 , 连接 , 点为射线上一个动点,若 , , 当与相似时,的长为 . 14. 如图,在直角梯形ABCD中, , , , , , 动点P从点A出发,以每秒2个单位的速度向点B运动,运动到B点停止,若以点P,A,D为顶点的三角形与相似时,运动时间 .
14. 如图,在直角梯形ABCD中, , , , , , 动点P从点A出发,以每秒2个单位的速度向点B运动,运动到B点停止,若以点P,A,D为顶点的三角形与相似时,运动时间 . 15. 在ΔABC 中,AC=4,BC=2. 点 D 在射线 AB 上,在构成的图形中,ΔACD 为等腰三角形,且存在两个互为相似的三角形,则 CD 的长是.
15. 在ΔABC 中,AC=4,BC=2. 点 D 在射线 AB 上,在构成的图形中,ΔACD 为等腰三角形,且存在两个互为相似的三角形,则 CD 的长是.三、解答题(共5题,共50分)
-
16. 如图,在中, , , , 动点P从点A开始沿着边AB向点B以1cm/s的速度移动,动点Q从点B开始沿着边BC向点C以2cm/s的速度移动.若P、Q两点同时开始运动,当点P运动到点B时停止,点Q也随之停止.设运动时间为 .
 (1)、当移动几秒时,的面积为?(2)、当移动几秒时,以B、P、Q为顶点的三角形与相似?17. 如图,直线与轴,轴分别相交于 , 两点,与双曲线相交于点 , 轴于点 , 且 , 点的坐标为 .
(1)、当移动几秒时,的面积为?(2)、当移动几秒时,以B、P、Q为顶点的三角形与相似?17. 如图,直线与轴,轴分别相交于 , 两点,与双曲线相交于点 , 轴于点 , 且 , 点的坐标为 . (1)、求一次函数和双曲线的解析式;(2)、若点为双曲线上点右侧的一点,且轴于 , 当时,求点的坐标.18. 如图,抛物线y=ax 2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.
(1)、求一次函数和双曲线的解析式;(2)、若点为双曲线上点右侧的一点,且轴于 , 当时,求点的坐标.18. 如图,抛物线y=ax 2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B. (1)、求抛物线的表达式;(2)、设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;(3)、点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似.若存在,求出点E的坐标;若不存在,请说明理由.19. 如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象交x轴于A(4,0),B(-1,0)两点,交y轴于点C,连接AC.
(1)、求抛物线的表达式;(2)、设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;(3)、点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似.若存在,求出点E的坐标;若不存在,请说明理由.19. 如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象交x轴于A(4,0),B(-1,0)两点,交y轴于点C,连接AC. (1)、填空:该抛物线的函数解析式为 , 其对称轴为直线;(2)、若P是抛物线在第一象限内图象上的一动点,过点P作x轴的垂线,交AC于点Q,试求线段PQ的最大值;(3)、在(2)的条件下,当线段PQ最大时,在x轴上有一点E(不与点O,A重合),且EQ=EA,在x轴上是否存在点D,使得△ACD与△AEQ相似?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.20. 如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A的坐标为 , 点B的坐标为 .
(1)、填空:该抛物线的函数解析式为 , 其对称轴为直线;(2)、若P是抛物线在第一象限内图象上的一动点,过点P作x轴的垂线,交AC于点Q,试求线段PQ的最大值;(3)、在(2)的条件下,当线段PQ最大时,在x轴上有一点E(不与点O,A重合),且EQ=EA,在x轴上是否存在点D,使得△ACD与△AEQ相似?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.20. 如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A的坐标为 , 点B的坐标为 . (1)、求反比例函数与一次函数的解析式.(2)、结合图象,请直接写出不等式的解集.(3)、在y轴上是否存在一点P,使得与相似,且点P不与原点O重合?若存在,求出点P的坐标;若不存在,说明理由.
(1)、求反比例函数与一次函数的解析式.(2)、结合图象,请直接写出不等式的解集.(3)、在y轴上是否存在一点P,使得与相似,且点P不与原点O重合?若存在,求出点P的坐标;若不存在,说明理由.