2023年浙教版数学九年级上册4.3相似三角形 同步测试(基础版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,已知△ABC∽△DEF,若∠A=35°,∠B=65°,则∠F的度数是( )
 A、30° B、35° C、80° D、100°2. 如图,已知 , 若 , , , 则AC的长是( )
A、30° B、35° C、80° D、100°2. 如图,已知 , 若 , , , 则AC的长是( )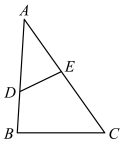 A、12 B、13 C、14 D、153. 如图所示, , , , 则的长为( )
A、12 B、13 C、14 D、153. 如图所示, , , , 则的长为( ) A、 B、2 C、3 D、44. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A、 B、2 C、3 D、44. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( ) A、AC2=AD•AB B、BC2=BD•BA C、CD2=AD•DB D、CD2=CA•CB5. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 , 另一个三角形的最短边长为 , 则它的最长边为( )A、 B、 C、 D、6. 已知的三边长分别为 , , , 的一边长为 , 如果这两个三角形相似,那么的另两边长可能是( )A、 , B、 , C、 , D、 ,7. 已知△ABC∽△DEF,AB:DE=3:1,AC=6,则DF为( )A、18 B、2 C、54 D、8. 已知与相似,又 , , 那么不可能是( )A、40° B、60° C、80° D、100°9. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
A、AC2=AD•AB B、BC2=BD•BA C、CD2=AD•DB D、CD2=CA•CB5. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 , 另一个三角形的最短边长为 , 则它的最长边为( )A、 B、 C、 D、6. 已知的三边长分别为 , , , 的一边长为 , 如果这两个三角形相似,那么的另两边长可能是( )A、 , B、 , C、 , D、 ,7. 已知△ABC∽△DEF,AB:DE=3:1,AC=6,则DF为( )A、18 B、2 C、54 D、8. 已知与相似,又 , , 那么不可能是( )A、40° B、60° C、80° D、100°9. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( ) A、= B、= C、= D、=10. 如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )
A、= B、= C、= D、=10. 如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )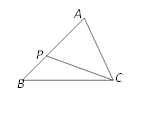 A、45° B、50° C、55° D、60°
A、45° B、50° C、55° D、60°二、填空题(每空4分,共24分)
-
11. 如图,△ABC∽△DAC,∠B=28°,∠D=140°,则∠BAD的度数为.
 12. 如图, , , , 则.
12. 如图, , , , 则. 13. 如图,已知△ABC∽△ADE,AD=6,BD=3,DE=4,则BC= .
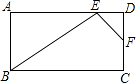
13. 如图,已知△ABC∽△ADE,AD=6,BD=3,DE=4,则BC= .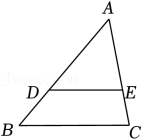 14. 如图所示,∠ACB=∠ADC=90°,AB=5,AC=4,若△ABC∽△ACD,则AD。
14. 如图所示,∠ACB=∠ADC=90°,AB=5,AC=4,若△ABC∽△ACD,则AD。 15. 如图,点C、D在线段AB上,△PCD是等边三角形.当△ACP∽△PDB时,∠APB=°.
15. 如图,点C、D在线段AB上,△PCD是等边三角形.当△ACP∽△PDB时,∠APB=°. 16. 已知:△ABC∽△DEF,且∠A=∠D,AB=8,AC=6,DE=2,那么DF= .
16. 已知:△ABC∽△DEF,且∠A=∠D,AB=8,AC=6,DE=2,那么DF= .三、解答题(共8题,共66分)
-
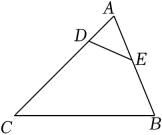
17. 如图,已知△ABC∽△ADE,AB=15,BD=3,BC=12,求DE的长.
 18. 如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长.
18. 如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长. 19. 如图,分别是、上的点, , , , , , 求的长和的度数.
19. 如图,分别是、上的点, , , , , , 求的长和的度数.