2023年浙教版数学九年级上册4.2 平行线分线段成比例 同步测试(提升版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图, , , 相交于点若 , , :( )
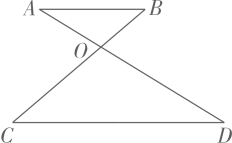 A、1:2 B、1:4 C、2:1 D、4:12. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( )
A、1:2 B、1:4 C、2:1 D、4:12. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( ) A、 B、 C、 D、3. 如图, , 直线与 , , 分别交于点和点 , 若 , , 则DE的长是( )
A、 B、 C、 D、3. 如图, , 直线与 , , 分别交于点和点 , 若 , , 则DE的长是( ) A、8 B、6 C、4 D、104. 如图,已知 , , , 则的长为( )
A、8 B、6 C、4 D、104. 如图,已知 , , , 则的长为( )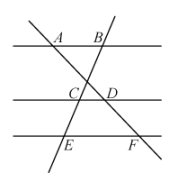 A、2 B、4 C、9 D、105. 如图,已知直线 , 直线 , 分别交直线a,b,c于A,B,C和D,E,F, , , , 则的长为( )
A、2 B、4 C、9 D、105. 如图,已知直线 , 直线 , 分别交直线a,b,c于A,B,C和D,E,F, , , , 则的长为( ) A、15 B、12 C、10 D、86. 如图,在中,已知点D,E分别是边AC,BC上的点, , 且 , 则等于( )
A、15 B、12 C、10 D、86. 如图,在中,已知点D,E分别是边AC,BC上的点, , 且 , 则等于( ) A、5:8 B、3:8 C、3:5 D、2:57. 如图,AB∥CD∥EF,AF与BE相交于点G,若AG=2,GD=1,DF=5,则的值是( )
A、5:8 B、3:8 C、3:5 D、2:57. 如图,AB∥CD∥EF,AF与BE相交于点G,若AG=2,GD=1,DF=5,则的值是( ) A、 B、 C、 D、8. 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
A、 B、 C、 D、8. 如图,已知AB∥CD∥EF,那么下列结论中正确的是( ) A、 B、 C、 D、9. 如图,是的外接圆,交于点E,垂足为点D,、的延长线交于点F.若 , , 则的长是( )
A、 B、 C、 D、9. 如图,是的外接圆,交于点E,垂足为点D,、的延长线交于点F.若 , , 则的长是( ) A、19 B、20 C、21 D、2210. 如图,在平行四边形ABCD中,E为的中点, , 在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A、19 B、20 C、21 D、2210. 如图,在平行四边形ABCD中,E为的中点, , 在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( ) A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题(每空4分,共20分)
-
11. 五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图, , , 为直线与五线谱的横线相交的三个点,则的值是.
 12. 如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,则FN:ND= .
12. 如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,则FN:ND= . 13. 矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则BF=.
13. 矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则BF=. 14. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
14. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .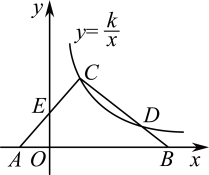 15. 如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值
15. 如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值
三、解答题(共9题,共70分)
-
16. 图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的顶点均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹,不要求写出画法.
 (1)、在图①中的线段BC上找一点O,使BO=CO.(2)、在图②中画一条线段MN、将线段AB分为3:4两部分,(要求:点M、N均在格点上)17. 如图,过点的直线与轴,轴分别交于点 , 两点,且 , 过点作轴,垂足为点 , 交反比例函数的图象于点 , 连接 , 的面积为6.
(1)、在图①中的线段BC上找一点O,使BO=CO.(2)、在图②中画一条线段MN、将线段AB分为3:4两部分,(要求:点M、N均在格点上)17. 如图,过点的直线与轴,轴分别交于点 , 两点,且 , 过点作轴,垂足为点 , 交反比例函数的图象于点 , 连接 , 的面积为6. (1)、求k的值和点D的坐标;(2)、如图,连接 , , 点在直线上,且位于第二象限内,若的面积是面积的2倍,求点的坐标.18. 如图,已知AD∥BE∥CF,它们依次交直线l1 , l2 , 于点A,B,C和点D,E,F.
(1)、求k的值和点D的坐标;(2)、如图,连接 , , 点在直线上,且位于第二象限内,若的面积是面积的2倍,求点的坐标.18. 如图,已知AD∥BE∥CF,它们依次交直线l1 , l2 , 于点A,B,C和点D,E,F. (1)、如果AB=6,BC=8,DF=7,求EF的长.(2)、如果AB:AC=2:5,EF=9,线段x是线段DE和线段DF的比例中项,求x的值.19. 如图,AB是的直径,弦于点E,F是上一点,连结AF并延长,与CD的延长线交于点G.连结FD,FC,AC.
(1)、如果AB=6,BC=8,DF=7,求EF的长.(2)、如果AB:AC=2:5,EF=9,线段x是线段DE和线段DF的比例中项,求x的值.19. 如图,AB是的直径,弦于点E,F是上一点,连结AF并延长,与CD的延长线交于点G.连结FD,FC,AC. (1)、求证:.(2)、若F是的中点, , 求GF的长.20. 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是劣弧 上一点,AG,DC的延长线交于点F.
(1)、求证:.(2)、若F是的中点, , 求GF的长.20. 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是劣弧 上一点,AG,DC的延长线交于点F. (1)、求证:∠FGC=∠AGD.(2)、若G是 的中点,CE= CF=2,求GF的长.21. 如图,四边形 是菱形, 是 的中点, 的垂线 交 于点 ,交 的延长线于点 .
(1)、求证:∠FGC=∠AGD.(2)、若G是 的中点,CE= CF=2,求GF的长.21. 如图,四边形 是菱形, 是 的中点, 的垂线 交 于点 ,交 的延长线于点 .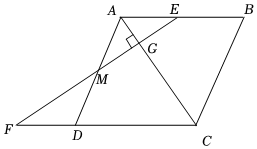 (1)、求证: ;(2)、连接 , .
(1)、求证: ;(2)、连接 , .求菱形 的周长;
若 ,求 的长.
22. 如图,在锐角三角形ABC中, ,以BC为直径作 ,分别交AB,AC于点D,E,点F是BD的中点,连接BE,CF交于点G. (1)、求证: .(2)、若 , ,求线段AD的长(用含r的代数式表示).(3)、若 ,探索CG与FG的数量关系,并说明理由.23. 如图,在矩形ABCD中,AB=12,BC=9,点E是射线AD上一动点且以每秒3个单位的速度从A出发向右运动,连结BE交AC于点F,作EM⊥BC于M交直线AC于N,设E点运动时间为1秒.
(1)、求证: .(2)、若 , ,求线段AD的长(用含r的代数式表示).(3)、若 ,探索CG与FG的数量关系,并说明理由.23. 如图,在矩形ABCD中,AB=12,BC=9,点E是射线AD上一动点且以每秒3个单位的速度从A出发向右运动,连结BE交AC于点F,作EM⊥BC于M交直线AC于N,设E点运动时间为1秒. (1)、若将线段EN绕点F旋转后恰好落在直线AB上,则t=(2)、当点E在线段AD上运动时,若FN=5t-3,求t的值.(3)、连结FM,点E在运动过程中,是否存在t的值,使△FMN为等腰三角形?若存在,请求出t的值:若不存在,请说明理由.24. 阅读材料解答问题:如图,在菱形ABCD中,AB=AC,过点C作一条直线,分别交AB,AD的延长线于M,N,则
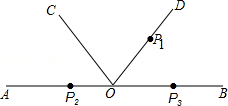
(1)、若将线段EN绕点F旋转后恰好落在直线AB上,则t=(2)、当点E在线段AD上运动时,若FN=5t-3,求t的值.(3)、连结FM,点E在运动过程中,是否存在t的值,使△FMN为等腰三角形?若存在,请求出t的值:若不存在,请说明理由.24. 阅读材料解答问题:如图,在菱形ABCD中,AB=AC,过点C作一条直线,分别交AB,AD的延长线于M,N,则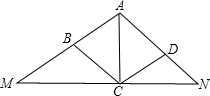 (1)、试证明: ;(2)、如图,O为直线AB上一点,OC,OD将平角AOB三等分,点P1 , P2 , P3分别在射线OA,OD,OB上,0P1=r1 , 0P2=r2 , OP3=r3 , r与r′分别满足 ,用直尺在图中分别作出长度r,r′的线段.
(1)、试证明: ;(2)、如图,O为直线AB上一点,OC,OD将平角AOB三等分,点P1 , P2 , P3分别在射线OA,OD,OB上,0P1=r1 , 0P2=r2 , OP3=r3 , r与r′分别满足 ,用直尺在图中分别作出长度r,r′的线段.