2023年浙教版数学九年级上册4.2 平行线分线段成比例 同步测试(培优版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在中,F是上一点,交于点E,的延长线交的延长线于点G, , , 则的长为( )
 A、4 B、6 C、8 D、102. 如图,在矩形中, , 延长至点 , 使得 , 以为直径的半圆交延长线于点.欧几里得在《几何原本》中利用该图得到结论:矩形的面积等于的平方(即).现连接并延长交于点 , 若 , 则与矩形的面积之比为( )
A、4 B、6 C、8 D、102. 如图,在矩形中, , 延长至点 , 使得 , 以为直径的半圆交延长线于点.欧几里得在《几何原本》中利用该图得到结论:矩形的面积等于的平方(即).现连接并延长交于点 , 若 , 则与矩形的面积之比为( )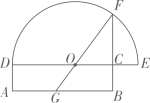 A、 B、 C、 D、3. 如图,是的中位线,点F在线段上, , 连接交于点E,下列说法错误的是( )
A、 B、 C、 D、3. 如图,是的中位线,点F在线段上, , 连接交于点E,下列说法错误的是( ) A、 B、 C、 D、4. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A、 B、 C、 D、4. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( ) A、 B、 C、6 D、5. 如图,在矩形 中, , , 平分 ,与对角线 相交于点N,F是线段 的中点,则 为( )
A、 B、 C、6 D、5. 如图,在矩形 中, , , 平分 ,与对角线 相交于点N,F是线段 的中点,则 为( ) A、 B、 C、 D、6. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、 B、 C、 D、6. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、7. 如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )
A、 B、 C、1 D、7. 如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )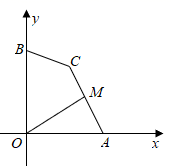 A、 B、 C、 D、8. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A、 B、 C、 D、8. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )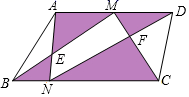 A、不变 B、一直变大 C、先减小后增大 D、先增大后减小9. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
A、不变 B、一直变大 C、先减小后增大 D、先增大后减小9. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( ) A、 B、13 C、 D、10. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、 B、13 C、 D、10. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )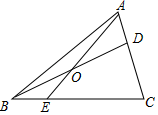 A、1:2 B、1:3 C、1:4 D、2:3
A、1:2 B、1:3 C、1:4 D、2:3二、填空题(每空4分,共24分)
-
11. 如图,正方形中,E为上一点,过B作于G,延长至点F使 , 延长交于点M,连接 , 若C为中点, , 则的长为 .
 12. 如图,矩形中,点 , 在轴上,交轴于点 , 点在上, , 连接交轴于点 , 过点作轴交于点 , 点在函数的图象上.若的面积为 , 则的值为 ;的面积与的面积差为 .
12. 如图,矩形中,点 , 在轴上,交轴于点 , 点在上, , 连接交轴于点 , 过点作轴交于点 , 点在函数的图象上.若的面积为 , 则的值为 ;的面积与的面积差为 .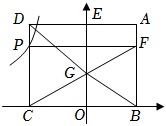 13. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 .
13. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 . 14. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.
14. 如图,在平行四边形ABCD中, , , ,分别以A,C为圆心,大于 的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为.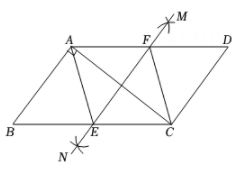 15. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是.
15. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是. 16. 如图,在边长为正方形 中,把边绕点逆时针旋转60°,得到线段 , 连接并延长交于 , 连接 , 则⊿的面积为 .
16. 如图,在边长为正方形 中,把边绕点逆时针旋转60°,得到线段 , 连接并延长交于 , 连接 , 则⊿的面积为 .
三、解答题(共8题,共66分)
-
17. 如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD .
 18. 如图,在矩形ABCD中,AB<AD,以点A为圆心,线段AD的长为半径画弧,与BC边交于点E,连接AE,过点D作DF⊥AE于点F.
18. 如图,在矩形ABCD中,AB<AD,以点A为圆心,线段AD的长为半径画弧,与BC边交于点E,连接AE,过点D作DF⊥AE于点F. (1)、求证:DF=AB.(2)、连接BF,若BE=6,CE=3,求线段BF的长.19. 如图,在的方格纸中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)、求证:DF=AB.(2)、连接BF,若BE=6,CE=3,求线段BF的长.19. 如图,在的方格纸中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合. (1)、在图1中画一条格点线段 , 使G,H分别落在边 , 上,且与互相平分.(2)、在图2上画一条格点线段 , 使M,N分别落在边 , 上,且要求分为两部分.20. 如图,中,于点E,点F是上一点,连接并延长交于点D,于点G,连接 .
(1)、在图1中画一条格点线段 , 使G,H分别落在边 , 上,且与互相平分.(2)、在图2上画一条格点线段 , 使M,N分别落在边 , 上,且要求分为两部分.20. 如图,中,于点E,点F是上一点,连接并延长交于点D,于点G,连接 . (1)、如图1,若 , 求证:;(2)、如图2,若 , 求线段的长.21. 如图,在中, , , , M是AB上的动点不与A、B重合 , 过点M作交AC于点N,以MN为直径作 , 并在内作内接矩形设.
(1)、如图1,若 , 求证:;(2)、如图2,若 , 求线段的长.21. 如图,在中, , , , M是AB上的动点不与A、B重合 , 过点M作交AC于点N,以MN为直径作 , 并在内作内接矩形设.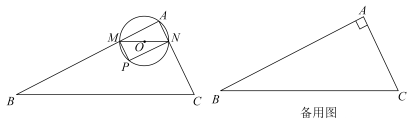 (1)、的面积 , ;用含x的代数式表示(2)、在动点M的运动过程中,设与四边形MNCB重合部分的面积为试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?22. 课本再现
(1)、的面积 , ;用含x的代数式表示(2)、在动点M的运动过程中,设与四边形MNCB重合部分的面积为试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?22. 课本再现思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在中,对角线 , 垂足为 .
求证:是菱形.
 (2)、知识应用:如图 , 在中,对角线和相交于点 , .
(2)、知识应用:如图 , 在中,对角线和相交于点 , .
①求证:是菱形;
②延长至点 , 连接交于点 , 若 , 求的值.
23. 已知:y关于x的函数 . (1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .
(1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,-是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
24. 在平面直角坐标系中,为坐标原点,抛物线经过点 , , 对称轴过点 , , 直线过点 , 且垂直于轴.过点的直线交抛物线于点、 , 交直线于点 , 其中点、Q在抛物线对称轴的左侧.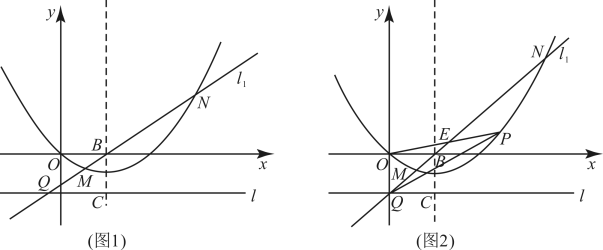 (1)求抛物线的解析式;(1)、如图1,当时,求点的坐标;(2)、如图2,当点恰好在轴上时,为直线下方的抛物线上一动点,连接、 , 其中交于点 , 设的面积为 , 的面积为 . 求的最大值.
(1)求抛物线的解析式;(1)、如图1,当时,求点的坐标;(2)、如图2,当点恰好在轴上时,为直线下方的抛物线上一动点,连接、 , 其中交于点 , 设的面积为 , 的面积为 . 求的最大值.