2023年浙教版数学九年级上册4.1 比例线段 同步测试(培优版)
试卷更新日期:2023-08-20 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 已知abc 0,而且 ,那么直线y=px+p一定通过( )
A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限2. 如图,点D、E分别在△ABC的边AB、AC上,若AD:BD=2:1,点G在DE上,DG:GE=1:2,连接BG并延长交AC于点F , 则AF:EF等于( )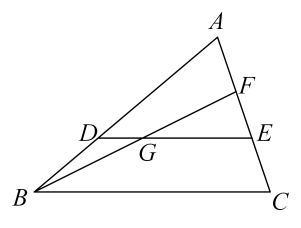 A、1:1 B、4:3 C、3:2 D、2:33. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为的雷锋雕像,那么该雕像的下部设计高度约是( )(精确到0.01.参考数据: , , )
A、1:1 B、4:3 C、3:2 D、2:33. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为的雷锋雕像,那么该雕像的下部设计高度约是( )(精确到0.01.参考数据: , , ) A、 B、 C、 D、4. 已知线段a、b,求作线段x,使 , 正确的作法是( )A、
A、 B、 C、 D、4. 已知线段a、b,求作线段x,使 , 正确的作法是( )A、 B、
B、 C、
C、 D、
D、 5. 已知:线段a,b,c,求作线段x,使x= , 以下作法正确的是( )A、
5. 已知:线段a,b,c,求作线段x,使x= , 以下作法正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 已知线段a,b,c,求作线段x,使 , 下列作法中正确的是( )A、
6. 已知线段a,b,c,求作线段x,使 , 下列作法中正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )A、100km B、2000m C、10km D、20km8. 已知点 是线段 上的一点,线段是和的比例中项,下列结论中,正确的是( )A、 B、 C、 D、9. 如图,将的圆周分成五等分(分点为A、B、C、D、E),依次隔一个分点相连,即成一个正五角星形.小张在制图过程中,惊讶于图形的奇妙,于是对图形展开了研究,得到:点M是线段AD、BE的黄金分割点,也是线段NE、AH的黄金分割点.在以下结论中,不正确的是( )
7. 在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )A、100km B、2000m C、10km D、20km8. 已知点 是线段 上的一点,线段是和的比例中项,下列结论中,正确的是( )A、 B、 C、 D、9. 如图,将的圆周分成五等分(分点为A、B、C、D、E),依次隔一个分点相连,即成一个正五角星形.小张在制图过程中,惊讶于图形的奇妙,于是对图形展开了研究,得到:点M是线段AD、BE的黄金分割点,也是线段NE、AH的黄金分割点.在以下结论中,不正确的是( ) A、 B、 C、 D、10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、 B、 C、 D、10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )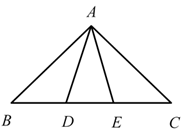 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 已知a、b、c、满足 ,从下列四点:① ;②(2,1);③ ;④(1,﹣1),中任意取一点恰好在正比例函数y=kx图象上的概率是.12. 在平面直角坐标系中,关于 的一次函数 ,其中常数k满足 ,常数b满足b>0且b是2和8的比例中项,则该一次函数 的解析式为 .13. 将2,3,4,6这四个数随机排列,排列结果记为 , , , .则 , , , 成比例的概率为.14. 如图,线段AB的长为1,C在AB上,D在AC上,且 , , , 则AE的长为 .
 15. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .16. 勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是 .
15. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .16. 勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是 .
三、解答题(共9题,共72分)
-
17. 若a、b、c是非零实数,且满足 ,直线y=kx+b经过点(4,0),求直线y=kx+b与两坐标轴所围成的三角形的面积.
18. 已知线段a,b,c满足 ,且a+2b+c=26.(1)、判断a,2b,c,b2是否成比例;(2)、若实数x为a,b的比例中项,求x的值.19.(1)、已知 , 求的值;(2)、将的图象先向左平移2个单位,再向下平移1个单位,求两次平移后所得到的抛物线解析式.20. 已知:a,b,c三个数满足关系式 .(1)、填空::4: .(2)、若 , 试求出的值.(3)、在(2)的基础上,若点是反比例函数的图像上的任意一点,过点向轴引垂线,垂足为 , 请直接写出的面积.21. 如图,在 中, ,BD是AC边上的高,已知BC=5厘米,AC=13厘米.求: (1)、(2)、(3)、再找两条线段和AB、BC构成比例线段.22. 如图,在线段AB上存在一点C,满足AC∶CB=CB∶AB=k.
(1)、(2)、(3)、再找两条线段和AB、BC构成比例线段.22. 如图,在线段AB上存在一点C,满足AC∶CB=CB∶AB=k. (1)、求k的值;(2)、如果三条线段a,b,c满足a∶b=b∶c=k,问这三条线段能否构成三角形,如果能,请指出三角形的形状;如果不能,请说明理由.
(1)、求k的值;(2)、如果三条线段a,b,c满足a∶b=b∶c=k,问这三条线段能否构成三角形,如果能,请指出三角形的形状;如果不能,请说明理由.
23. 如图1所示,点C把线段 分成 与 ,若 ,则称线段 被点C黄金分割(goldensection),点C叫做线段 的黄金分割点, 与 的比叫做黄金比.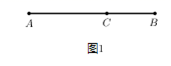 (1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C .
(1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C . (3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.24. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.
(3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.24. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.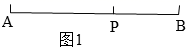
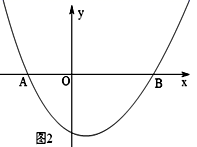 (1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.25. 如图,点B在线段AC上的黄金分割点,且AB>BC.
(1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.25. 如图,点B在线段AC上的黄金分割点,且AB>BC. (1)、设AC=2,完成下面填空
(1)、设AC=2,完成下面填空设AB=x,则BC=2﹣x
∵点B在线段AC上的黄金分割点,且AB>BC,
∴ , 可列方程为 ,
解得方程的根为 , 于是,AB的长为 .
(2)、在线段AC(如图1)上利用三角板和圆规画出点B的位置(保留作图痕迹,不写作法);(3)、若m、n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,①求证:(t+m)2=m2+n2;
②若两条线段的长分别为m、n(如图2),请画出一条长为t的线段(保留作图痕迹,不写作法).
