【备考2024】高考数学（函数版块）细点逐一突破训练：三角函数的应用

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 摩天轮常被当作一个城市的地标性建筑，如静安大悦城的“Sky Ring”摩天轮是上海首个悬臂式屋顶摩天轮.摩天轮最高点离地面高度106米，转盘直径56米，轮上设置30个极具时尚感的4人轿舱，拥有360度的绝佳视野.游客从离楼顶屋面最近的平台位置进入轿舱，开启后按逆时针匀速旋转t分钟后，游客距离地面的高度为h米， $h = - 28 c o s (\frac{π t}{6}) + 78$ .若在 $t_{1}$ ， $t_{2}$ 时刻，游客距离地面的高度相等，则 $t_{1} + t_{2}$ 的最小值为（　　）

A、6 B、12 C、18 D、24

查看试题解析
2. 位于登封市告成镇的观星台相当于一个测量日影的圭表．圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”）．当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．如图是一个根据郑州市的地理位置设计的圭表的示意图，已知郑州市冬至正午太阳高度角（即 $∠ A B C$ ）约为32.5°，夏至正午太阳高度角（即 $∠ A D C$ ）约为79.5°，圭面上冬至线与夏至线之间的距离（即 $D B$ 的长）为14米，则表高（即 $A C$ 的长）约为（）（其中 $t a n 32.5 ° \approx \frac{3}{5}$ ， $t a n 79.5 ° \approx \frac{27}{5}$ ）

A、9.27米 B、9.33米 C、9.45米 D、9.51米

查看试题解析
3. 如图，某摩天轮最高点距离地面高度为 $120$ $m$ ，转盘直径为 $110 m$ ，开启后按逆时针方向匀速旋转，旋转一周需要 $30$ $m i n$ .游客在座舱转到距离地面最近的位置进舱，开始转动 $t$ $m i n$ 后距离地面的高度为 $H$ $m$ ，则在转动一周的过程中，高度 $H$ 关于时间 $t$ 的函数解析式是（）

A、 $H = 55 c o s (\frac{π}{15} t - \frac{π}{2}) + 65 (0 \leq t \leq 30)$ B、 $H = 55 s i n (\frac{π}{15} t - \frac{π}{2}) + 65 (0 \leq t \leq 30)$ C、 $H = - 55 c o s (\frac{π}{10} t + \frac{π}{2}) + 65 (0 \leq t \leq 30)$ D、 $H = - 55 s i n (\frac{π}{10} t + \frac{π}{2}) + 65 (0 \leq t \leq 30)$

查看试题解析
4. 太阳高度角是太阳光线与地面所成的角（即太阳在当地的仰角）．设地球表面某地正午太阳高度角为 $θ$ ， $δ$ 为此时太阳直射点纬度， $φ$ 为当地纬度值，那么这三个量满足 $θ = 90 ° - | φ - δ |$ ．通州区某校学生科技社团尝试估测通州区当地纬度值（ $φ$ 取正值），选择春分当日（ $δ = 0 °$ ）测算正午太阳高度角．他们将长度为1米的木杆垂直立于地面，测量木杆的影长．分为甲、乙、丙、丁四个小组在同一场地进行，测量结果如下：
组别
甲组
乙组
丙组
丁组
木杆影长度（米）
0.82
0.80
0.83
0.85
则四组中对通州区当地纬度估测值最大的一组是（）

A、甲组 B、乙组 C、丙组 D、丁组

查看试题解析
5. 智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声，然后通过主动降噪芯片生成的声波来抵消噪声（如图）．已知噪声的声波曲线是 $y = 2 c o s 3 x$ ，通过主动降噪芯片生成的声波曲线是 $y = A s i n (ω x + φ)$ （其中 $A > 0 ， ω > 0 ， 0 \leq φ < 2 π$ ），则 $φ =$ （）

A、 $\frac{π}{2}$ B、π C、 $\frac{3 π}{2}$ D、 $\frac{π}{6}$

查看试题解析
6. 水车是我国劳动人民创造发明的一种灌溉工具，作为中国农耕文化的组成部分，充分体现了中华民族的创造力，见证了中国农业文明．水车的外形酷似车轮，在轮的边缘装有若干个水斗，借助水势的运动惯性冲动水车缓缓旋转，将水斗内的水逐级提升．某水车轮的半径为5米，圆心距水面的高度为4米，水车按逆时针方向匀速转动，每分钟转动2圈，当其中的一个水斗 $A$ 到达最高点时开始计时，设水车转动 $t$ （分钟）时水斗 $A$ 距离水面的高度（水面以上为正，水面以下为负）为 $f (t)$ （米），下列选项正确的是（）

A、 $f (t) = 5 c o s 4 π t + 4$ （ $t \geq 0$ ） B、 $f (t) = 5 s i n (π t + \frac{π}{2}) + 4$ （ $t \geq 0$ ） C、 $- \frac{1}{2}$ 是函数 $f (t)$ 的周期 D、在旋转一周的过程中，水斗 $A$ 距离水面高度不低于6.5米的时间为10秒．

查看试题解析
7. 2022年春节期间，G市某天从8~16时的温度变化曲线（如图）近似满足函数 $f (x) = 2 \sqrt{2} c o s (ω x + φ)$ （ $ω > 0$ ， $0 < φ < π$ ， $x \in [8 ， 16]$ ）的图像．下列说法正确的是（）

A、8～13时这段时间温度逐渐升高 B、8～16时最大温差不超过5℃ C、8～16时0℃以下的时长恰为3小时 D、16时温度为−2℃

查看试题解析
8. 已知函数 $f (x) = a s i n ω x + c o s ω x (a > 0 ， ω > 0)$ 的部分图象如图所示，其中 $| B C | = 2$ ，且 $△ A B C$ 的面积为 $2$ ，则下列函数值恰好等于 $a$ 的是（）

A、 $f (\frac{1}{3})$ B、 $f (\frac{5}{6})$ C、 $f (1)$ D、 $f (2)$

查看试题解析
9. 已知函数 $f (x) = 2 s i n (ω x + φ) + 1 (ω > 0 ， | φ | \leq \frac{π}{2})$ ，其图象与直线 $y = - 1$ 相邻两个交点的距离为 $π$ ，若 $\forall x \in (- \frac{π}{12} ， \frac{π}{3}) ， f (x) > 1$ 恒成立，则 $φ$ 的取值范围是（）

A、 $(\frac{π}{6} ， \frac{π}{3})$ B、 $[\frac{π}{12} ， \frac{π}{3}]$ C、 $[\frac{π}{12} ， \frac{π}{2}]$ D、 $[\frac{π}{6} ， \frac{π}{3}]$

查看试题解析
10. 红河州个旧市是一个风景优美的宜居城市，如图是个旧宝华公园的摩天轮，半径为20米，圆心O距地面的高度为25米，摩天轮运行时按逆时针匀速旋转，转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底，则摩天轮转动一周内具有最佳视觉效果的时间长度（单位：分钟）为（）

A、 $\frac{8}{3}$ B、3 C、 $\frac{10}{3}$ D、 $\frac{11}{3}$

查看试题解析

二、填空题

11. 如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15m，AC=25m，∠BCM=30°，则tanθ的最大值是．（仰角θ为直线AP与平面ABC所成角）

查看试题解析
12. 神舟十三号三位航天英雄在太空出差180余天后，顺利返回地面．如图，返回舱达到一定高度时，近似垂直落地，在下落过程中的某时刻位于点 $C$ ，预计垂直落在地面点 $D$ 处，在地面同一水平线上的A、B两个观测点，分别观测到点 $C$ 的仰角为15°，45°，若 $| A B | = 24$ 千米，则点 $C$ 距离地面的高度 $| C D |$ 约为千米（参考数据： $\sqrt{3} \approx 1.7$ ）．

查看试题解析
13. 我国古代数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明，后人称其为“赵爽弦图”，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，如图所示.记大正方形的面积为 $S_{1}$ ，小正方形的面积为 $S_{2}$ ，若 $S_{1} = 25 S_{2}$ ，则 $t a n ∠ A B E =$ .

查看试题解析
14. 在平面直角坐标系中，半径为1的圆 $C$ 与 $x$ 轴相切于原点 $O$ ，圆 $C$ 上有一定点 $P$ ，坐标是 $(1 ， 1)$ ．假设圆 $C$ 以 $\frac{π}{5}$ （单位长度）/秒的速度沿 $x$ 轴正方向匀速滚动，那么当圆 $C$ 滚动 $t$ 秒时，点 $P$ 的横坐标 $x =$ ．（用 $t$ 表示）

查看试题解析
15. 一个单摆作简谐振动位移-时间图象如图所示，S表示离开O的位移（单位：cm），t表示振动的时间（单位：s），则该简谐振动的振幅为cm，振动的最小正周期为s．

查看试题解析
16. 筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中得到使用. 明朝科学家徐光启在《农政全书》中用图1描绘了筒车的工作原理.假定在水流稳定的情况下，筒车上的每一个盛水筒都做匀速圆周运动.
如图2，将筒车抽象为一个几何图形（圆），以筒车转轮的中心 $O$ 为原点，过点 $O$ 的水平直线为 $x$ 轴建立如图直角坐标系 $x O y$ . 已知一个半径为1.6m的筒车按逆时针方向每30s匀速旋转一周， $O$ 到水面的距离为0.8m.规定：盛水筒 $M$ 对应的点 $P$ 从水中浮现（ $P_{0}$ 时的位置）时开始计算时间，且设盛水筒 $M$ 从点 $P_{0}$ 运动到点 $P$ 时所经过的时间为 $t$ （单位：s），且此时点 $P$ 距离水面的高度为 $d$ （单位：m）（在水面下则 $d$ 为负数），则 $d$ 关于 $t$ 的函数关系式为，在水轮转动的任意一圈内，点 $P$ 距水面的高度不低于1.6m的时长为s.

查看试题解析
17. 用一张A4纸围绕半径为rcm的石膏圆柱体包裹若干圈，然后用裁纸刀将圆柱体切为两段，如图①所示．设圆柱体母线与截面的夹角为 $θ$ （0°＜ $θ$ ＜90°），如图②．将其中一段圆柱体外包裹的A4纸展开铺平，如果忽略纸的厚度造成的误差，我们会发现剪裁边缘形成的曲线是正弦型曲线，如图③．建立适当的坐标系后，这条曲线的解析式可设为 $f (x) = A \sin ω x (A > 0 ， ω > 0)$ ，若f(x)的最小正周期为 $2 π$ ，则r＝cm，此时，当 $θ$ ＝时，可使f(x)的值域为 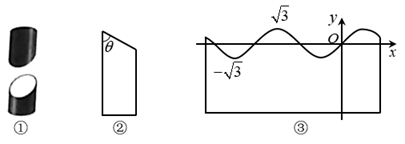$[- \sqrt{3} ， \sqrt{3}]$ ．

查看试题解析
18. 已知函数 $f (x) = \sin (ω x - \frac{π}{5}) + \frac{1}{2} (ω > 0)$ ，若函数 $f (x)$ 的最小正周期为 $\frac{π}{2}$ ，则 $ω =$ ，若 $ω = 2$ ，则函数 $y = | f (x) |$ 的最小正周期为.

查看试题解析
19. 在 $△ A B C$ 中，两直角边和斜边分别为a，b，c，若 $a + b = c x$ 则实数x的取值范围是.

查看试题解析
20. 一货轮航行到M处，测得灯塔S在货轮的北偏东15°，与灯塔S相距20海里，随后货轮继续沿正西方向航行30分钟到达N处后，又测得灯塔在货轮的北偏东45°，则货轮的速度为海里/时．

查看试题解析
21. 如图，一船自西向东匀速航行，上午10时到达一座灯塔P的南偏西75°距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船的航行速度为海里/小时．

查看试题解析
22. 某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos[ $\frac{π}{6}$ （x﹣6）]（x=1，2，3，…，12）来表示，已知6月份的月平均气温最高为28℃，12月份的月平均气温最低为18℃，则10月份的平均气温值为℃．

查看试题解析

三、解答题

23.

(1)、求简谐振动 $y = s i n x + c o s x$ 的振幅、周期和初相位 $φ (φ \in [0 ， 2 π))$ ；

(2)、若函数 $y = s i n \frac{1}{2} x + \frac{1}{2} c o s x$ 在区间 $(0 ， m)$ 上有唯一的极大值点，求实数m的取值范围；

(3)、设 $a > 0$ ， $f (x) = s i n a x - a s i n x$ ，若函数 $y = f (x)$ 在区间 $(0 ， π)$ 上是严格增函数，求实数a的取值范围．

查看试题解析
24. 某展览会有四个展馆，分别位于矩形ABCD的四个顶点A、B、C、D处，现要修建如图中实线所示的步道（宽度忽略不计，长度可变）把这四个展馆连在一起，其中 $A B = 8$ 百米， $A D = 6$ 百米，且 $A E = D E = B F = C F$ .

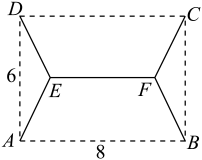(1)、试从各段步道的长度与图中各角的弧度数中选择某一变量作为自变量x，并求出步道的总长y（单位：百米）关于x的函数关系式；

(2)、求步道的最短总长度（精确到0.01百米）.

查看试题解析
25. 某地区的一种特色水果上市时间11个月中，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数：① $f (x) = p \cdot q^{x} ；$ ② $f (x) = p x^{2} + q x + 1 ；$ ③ $f (x) = A s i n (\frac{π}{4} x - \frac{π}{4}) + B$ (以上三式中 $p ， q ， A ， B$ 均为非零常数， $q > 1$ .)

(1)、为准确研究其价格走势，应选哪种价格模拟函数，为什么?

(2)、若 $f (3) = 8 ， f (7) = 4 ，$ 求出所选函数 $f (x)$ 的解析式(注：函数的定义域是 $[0 ， 10]$ ，其中 $x = 0$ 表示 $1$ 月份， $x = 1$ 表示2月份， $⋯ ⋯$ ，以此类推)，为保证果农的收益，打算在价格在5元以下期间积极拓宽外销渠道，请你预测该水果在哪几个月份要采用外销策略？

查看试题解析
26. 已知函数 $f (x) = \sin (ω x + φ) + m (ω > 0 ， - \frac{π}{2} < φ < 0)$ 满足下列4个条件中的3个，4个条件依次是：① $ω = 2$ ，②周期 $T = π$ ，③过点 $(0 ， 0)$ ，④ $f (\frac{π}{3}) = \frac{3}{2}$ .

(1)、试写出能确定 $f (x)$ 解析式的3个条件的序号(不需要说明理由)，并求 $f (x)$ 的解析式；

(2)、求（1）中函数 $f (x)$ 的图象与直线 $y = 1$ 交点间的最短距离.

查看试题解析
27. 某艺术品公司欲生产一款迎新春工艺礼品，该礼品是由玻璃球面和该球的内接圆锥组成，圆锥的侧面用于艺术装饰，如图1.为了便于设计，可将该礼品看成是由圆 $O$ 及其内接等腰三角形 $A B C$ 绕底边 $B C$ 上的高所在直线 $A O$ 旋转180°而成，如图2.已知圆 $O$ 的半径为 $10 c m$ ，设 $∠ B A O = θ ， 0 < θ < \frac{π}{2}$ ，圆锥的侧面积为 $S c m^{2}$ .

(1)、求 $S$ 关于 $θ$ 的函数关系式；

(2)、为了达到最佳观赏效果，要求圆锥的侧面积 $S$ 最大.求 $S$ 取得最大值时腰 $A B$ 的长度.

查看试题解析
28. 如图扇形AOB是一个观光区的平面示意图，其中∠AOB的圆心角为 $\frac{2 π}{3}$ ，半径OA为1km，为了便于游客观光休闲，拟在观光区内铺设一条从入口A到出口B的观光道路，道路由圆弧AC、线段CD及线段BD组成．其中D在线段OB上，且CD∥AO，设∠AOC=θ，

(1)、用θ表示CD的长度，并写出θ的取值范围．

(2)、当θ为何值时，观光道路最长？

查看试题解析
29. 如图，经过村庄A有两条夹角60°为的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M，N（异于村庄A），要求PM=PN=MN=2（单位：千米）．记∠AMN=θ．

(1)、将AN，AM用含θ的关系式表示出来；

(2)、如何设计（即AN，AM为多长时），使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离AP最大）？

查看试题解析
30. 如图，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asinωx（A＞0，ω＞0）x∈[0，4]的图象，且图象的最高点为 $S (3 ， 2 \sqrt{3})$ ；赛道的后一部分为折线段MNP，为保证参赛运动员的安全，限定∠MNP=120°

(1)、求A，ω的值和M，P两点间的距离；

(2)、应如何设计，才能使折线段赛道MNP最长？

查看试题解析
31. 在水域上建一个演艺广场，演艺广场由看台Ⅰ，看台Ⅱ，三角形水域ABC，及矩形表演台BCDE四个部分构成（如图），看台Ⅰ，看台Ⅱ是分别以AB，AC为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍，矩形表演台BCDE 中，CD=10米，三角形水域ABC的面积为 $400 \sqrt{3}$ 平方米，设∠BAC=θ．

(1)、求BC的长（用含θ的式子表示）；

(2)、若表演台每平方米的造价为0.3万元，求表演台的最低造价．

查看试题解析
32.
一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的3倍．假设缉私艇和走私船均按直线方向以最大航速航行．（参考数据： $\sin 17$ ° $\approx \frac{\sqrt{3}}{6}$ ， $\sqrt{33} \approx 5.7446$ ）

(1)、若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；

(2)、问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．

查看试题解析

组别	甲组	乙组	丙组	丁组
木杆影长度（米）	0.82	0.80	0.83	0.85