华师大版数学八年级上册12.3 乘法公式同步练习（提升卷）

试卷更新日期：2023-08-18 类型：同步测试

进入出卷网下载

一、选择题

1. 下列多项式，能用平方差公式分解的是（）

A、 $- x^{2} - 4 y^{2}$ B、 $9 x^{2} + 4 y^{2}$ C、 $- x^{2} + 4 y^{2}$ D、 $x^{2} + (- 2 y)^{2}$

查看试题解析
2. 已知 $a^{2} - b^{2} = 16$ ， $a - b = 2$ ，则 $a + b$ 等于（）

A、 $- 8$ B、 $- 6$ C、4 D、8

查看试题解析
3. 下列运算正确的是（）

A、 $2 a^{2} + a^{3} = 3 a^{5}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(2 a^{2})}^{3} = 8 a^{6}$ D、 $(a + 2)^{2} = a^{2} + 4$

查看试题解析
4. 下列各式中，能用平方差公式分解因式的是（）

A、 $x^{2} - x$ B、 $x^{2} + 2 x - 1$ C、 $x^{2} + y^{2}$ D、 $x^{2} - 1$

查看试题解析
5. 若a+x²＝2020，b+x²＝2021，c+x²＝2022，则a²+b²+c²-ab-bc-ca的值为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 设 $a = \sqrt{7} - 1$ ，则 $3 a^{3} + 12 a^{2} - 6 a - 12 =$ （）

A、24 B、25 C、 $4 \sqrt{7} + 10$ D、 $4 \sqrt{7} + 12$

查看试题解析
7. 已知a-b＝3，ab＝2，则a²-ab+b²的值为（）

A、9 B、13 C、11 D、8

查看试题解析
8. 已知 $n$ 为自然数，则 ${(n + 1)}^{2} - {(n - 3)}^{2}$ 一定能被下列哪个数整除？（）

A、5 B、6 C、7 D、8

查看试题解析
9. 若 $a + b = 2$ ，则 $a^{2} - b^{2} + 4 b$ 的值为（）

A、2 B、3 C、4 D、6

查看试题解析
10. 计算： $\frac{5}{2} a \times 100 1^{2} - \frac{5}{2} a \times 99 9^{2} =$ （）

A、5000a B、1999a C、10001a D、10000a

查看试题解析

二、填空题

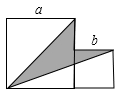
11. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 $A = a^{2} + a$ ，请结合你所学知识，判断下列说法：①当 $a = - 2$ 时， $A = 2$ ；②无论a取任何实数，不等式 $A + \frac{1}{4} \geq 0$ 恒成立；③若 $A - 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} = 4$ ；正确的有.

查看试题解析
12. 若 $a - b = 5$ ， $a^{2} + b^{2} = 13$ ，则ab＝．

查看试题解析
13. 若 ${(x + y)}^{2} = 12$ ， ${(x - y)}^{2} = 8$ ，则xy= ．

查看试题解析
14. 若a≠b，且a²-a＝b²-b，则a+b＝．

查看试题解析
15. 如图，两个正方形边长分别为a、b，且满足 $a + b = 6$ ， $a b = 4$ ，图中阴影部分的面积为.

查看试题解析

三、综合题

16. 如图1是一个长为 $4 a$ 、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）

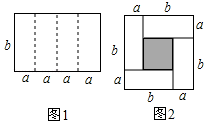(1)、观察图2请你写出 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5 ， x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 $(2019 - m)^{2} + (m - 2020)^{2} = 7$ ，求 $(2019 - m)$ $(m - 2020)$ 的值.

查看试题解析
17. 认真观察图形，解答下列问题：

(1)、根据图①中的条件，试用两种不同方法表示两个阴影图形的面积的和．
方法1：；方法2：．

(2)、从中你能发现什么结论？请用等式表示出来：；

(3)、利用（2）中结论解决下面的问题：如图②，两个正方形边长分别为m，n，如果m＋n＝mn＝4，求阴影部分的面积．

查看试题解析
18.

(1)、如图1，将边长为 $(a + b)$ 的正方形面积分成四部分，可以验证的乘法公式是；（填序号）
① ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ；② ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$
③ $(a + b) (a - b) = a^{2} - b^{2}$ ；④ $a (a + b) = a^{2} + a b$

(2)、利用上面得到的乘法公式解决问题：
①已知 $a + b = 5$ ， $a b = 3$ ，求 $a^{2} + b^{2}$ 的值；
②如图2，点C是线段 $A B$ 上的一点，以 $A C$ 、 $B C$ 为边向两边作正方形，连接 $B D$ ，若 $A B = 7$ ，两正方形的面积和 $S_{1} + S_{2} = 23$ ，求 $△ B C D$ 的面积．

查看试题解析
19. 问题背景
如图，图1，图2分别是边长为 $(a + b)$ ， a的正方形，由图1易得 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ．
　　　
类比探究
类比由图1易得公式 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ 的方法，依据图2中的已知条件推导出完全平方的另一个公式．
解决问题

(1)、计算： ${(2 m - n)}^{2} =$ ；

(2)、运用完全平方公式计算： $10 5^{2}$ ；

(3)、已知 ${(x + y)}^{2} = 12$ ， $x y = 2$ ，求 ${(x - y)}^{2}$ 的值．

查看试题解析
20. 下列方框中的内容是小宇分解因式的解题步骤．
分解因式： $(x^{2} + 4 x + 3) (x^{2} + 4 x + 5) + 1$ ．
解：设 $y = x^{2} + 4 x$ ．
原式 $= (y + 3) (y + 5) + 1$ （第一步）
$= y^{2} + 8 y + 16$ （第二步）
$= {(y + 4)}^{2}$ （第三步）
$= {(x^{2} + 4 x + 4)}^{2}$ ．（第四步）
请回答下列问题：

(1)、小宇分解因式中第二步到第三步运用了____．

A、提公因式法 B、平方差公式法 C、两数和的完全平方公式法 D、两数差的完全平方公式法

(2)、小宇得到的结果能否继续因式分解？若能，直接写出分解因式的结果；若不能，请说明理由．

(3)、请对多项式 $(x^{2} + 2 x + 6) (x^{2} + 2 x - 4) + 25$ 进行因式分解．

查看试题解析

华师大版数学八年级上册12.3 乘法公式 同步练习（提升卷）

一、选择题

二、填空题

三、综合题

华师大版数学八年级上册12.3 乘法公式同步练习（提升卷）