华师大版数学八年级上册12.5 因式分解 同步练习(提升卷)
试卷更新日期:2023-08-18 类型:同步测试
一、选择题
-
1. 下列变形从左到右是因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2+2x+1=x(x+2)+1 C、-2x(x+y)=-2x2-2xy D、x2-12x+36=(x-6)22. 下列因式分解正确的是( )A、 B、 C、 D、3. 若a2+2ab+b2-c2=10,a+b+c=5,则a+b-c的值是( )A、2 B、5 C、20 D、94. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 下列各式从左到右的变形,是因式分解的是( )A、 B、 C、 D、7. 下列因式分解正确的是( )A、 B、 C、 D、8. 将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式.例如,由图(1)可得等式: . 将图(2)所示的卡片若干张进行拼图,可以将二次三项式分解因式为( )
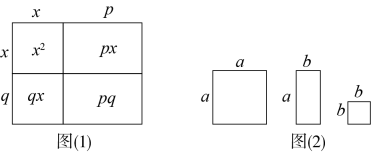 A、 B、 C、 D、9. 多项式的公因式是( )A、 B、 C、 D、10. 设 ( 的自然数),如果 是整数,n的值有( )A、2个 B、3个 C、4个 D、5个
A、 B、 C、 D、9. 多项式的公因式是( )A、 B、 C、 D、10. 设 ( 的自然数),如果 是整数,n的值有( )A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 分解因式: .12. 分解因式: ,13. 因式分解: .14. 把多项式分解因式时,应提取的公因式是 .15. 在实数范围内分解因式: .
三、综合题
-
16. 阅读下列材料:
在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.
下面是小涵同学用换元法对多项式(x2-4x+1)(x2-4x+7)+9进行因式分解的过程.
解:设x2-4x=y
原式=(y+1)(y+7)+9(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
请根据上述材料回答下列问题:
(1)、小涵同学的解法中,第二步到第三步运用了因式分解的 ;A、提取公因式法 B、平方差公式法 C、完全平方公式法(2)、老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;(3)、请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.17. 下面是某同学对多项式进行因式分解的过程.解:设 ,
原式
回答下列问题:
(1)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”),若不彻底,请写出因式分解的最后结果;(2)、以上方法叫做“换元法”.请你模仿以上方法对进行因式分解.18. 王老师在黑板上写下了四个算式:①;
②;
③;
④;
……
认真观察这些算式,并结合你发现的规律,解答下列问题:
(1)、 ;.(2)、小华发现上述算式的规律可以用文字语言概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为2n+1和2n-1(n为正整数),请你用含有n的算式验证小华发现的规律.19. 如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且 . (1)、观察图形,可以发现代数式可以因式分解为 .(2)、若图中阴影部分的面积为20平方厘米,大长方形纸板的周长为24厘米,求图中空白部分的面积.20. 将两个大小不一的等腰直角三角形按如图①,②的方式摆放,设两个三角形的直角边长分别为 , ,图②中阴影部分的面积为 .
(1)、观察图形,可以发现代数式可以因式分解为 .(2)、若图中阴影部分的面积为20平方厘米,大长方形纸板的周长为24厘米,求图中空白部分的面积.20. 将两个大小不一的等腰直角三角形按如图①,②的方式摆放,设两个三角形的直角边长分别为 , ,图②中阴影部分的面积为 .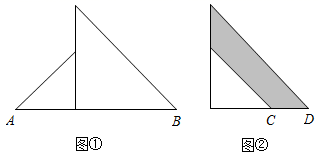 (1)、用含 , 的代数式表示图②中阴影部分的面积;(2)、将(1)中的代数式因式分解;(3)、若 , ,用含 , 的式子表示图②中阴影部分的面积.
(1)、用含 , 的代数式表示图②中阴影部分的面积;(2)、将(1)中的代数式因式分解;(3)、若 , ,用含 , 的式子表示图②中阴影部分的面积.