【备考2024】高考数学（函数版块）细点逐一突破训练：二分法与求方程近似解

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 已知函数 $f (x) = {\begin{array}{l} x^{3} ， & x ⩾ 0 ， \\ - x ， & x < 0. \end{array}$ 若函数 $g (x) = f (x) - | k x^{2} - 2 x | (k \in R)$ 恰有4个零点，则k的取值范围是（）

A、 $(- \infty ， - \frac{1}{2}) \cup (2 \sqrt{2} ， + \infty)$ B、 $(- \infty ， - \frac{1}{2}) \cup (0 ， 2 \sqrt{2})$ C、 $(- \infty ， 0) \cup (0 ， 2 \sqrt{2})$ D、 $(- \infty ， 0) \cup (2 \sqrt{2} ， + \infty)$

查看试题解析
2. 用二分法求方程 $l o g_{4} x - \frac{1}{2 x} = 0$ 近似解时，所取的第一个区间可以是（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析
3. 公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率 $π$ ，他从单位圆内接正六边形算起，令边数一倍一倍地增加，即12，24，48，…，192，…，逐个算出正六边形，正十二边形，正二十四边形，…，正一百九十二边形，…的面积，这些数值逐步地逼近圆面积，刘徽算到了正一百九十二边形，这时候 $π$ 的近似值是3.141024，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无穷，这种思想极其重要，对后世产生了巨大影响.按照上面“割圆术”，用正二十四边形来估算圆周率，则 $π$ 的近似值是（）（精确到 $0.01$ ）.（参考数据 $\sin 15 ° \approx 0.2588$ ）

A、3.14 B、3.11 C、3.10 D、3.05

查看试题解析
4. 已知定义在R上的函数f（x）的图象的对称轴为x=﹣4，且当x≥﹣4时，f（x）=2^x﹣3，若函数f（x）在区间（k﹣1，k）（k∈Z）上有零点，则k的值为（　　）

A、﹣8或﹣7 B、﹣8或2 C、2或﹣9 D、﹣2或﹣8

查看试题解析
5. 关于函数 $f (x) = \frac{x^{2} + 2 x - 2}{e^{x}}$ ，有如下列结论：①函数 $f (x)$ 有极小值也有最小值；②函数 $f (x)$ 有且只有两个不同的零点；③当 $- 2 e^{2} < k < \frac{6}{e^{2}}$ 时， $f (x) = k$ 恰有三个实根；④若 $x \in [0 ， t]$ 时， $f {(x)}_{m a x} = \frac{6}{e^{2}}$ ，则 $t$ 的最小值为 $2$ ．其中正确结论的个数是（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
6. 已知拋物线 $C ： y^{2} = x$ ，点 $A ， B$ 均在抛物线 $C$ 上，点 $P (0 ， 3)$ ，则（）

A、直线 $P A$ 的斜率可能为 $\frac{1}{10}$ B、线段 $P A$ 长度的最小值为 $\sqrt{5}$ C、若 $P ， A ， B$ 三点共线，则存在唯一的点 $B$ ，使得点 $A$ 为线段 $P B$ 的中点 D、若 $P ， A ， B$ 三点共线，则存在两个不同的点 $B$ ，使得点 $A$ 为线段 $P B$ 的中点

查看试题解析
7. 已知 $f (x) = {\begin{array}{l} - x^{2} + 2 x + 1 ， x < 0 \\ \frac{x}{e^{x}} ， x \geq 0 \end{array}$ ，若关于 $x$ 的方程 $4 e f^{2} (x) - a f (x) + \frac{1}{e} = 0$ 恰好有6个不同的实数解，则 $a$ 的取值可以是（）

A、 $\frac{17}{4}$ B、 $\frac{19}{4}$ C、 $\frac{21}{4}$ D、 $\frac{23}{4}$

查看试题解析
8. 已知函数 $f (x) = {\begin{array}{l} (x + 1) l n x ， x > 0 \\ k x - l n (- x) + k ， x < 0 \end{array}$ ，若关于x的方程 $f (- x) = - f (x)$ 有且仅有四个相异实根，则实数 $k$ 的取值范围为（）

A、 $(0 ， \frac{1}{e - 1})$ B、 $(1 ， + \infty)$ C、 $(0 ， \frac{1}{e - 1}) \cup (1 ， + \infty)$ D、 $(0 ， 1) ∪ (1 ， + \infty)$

查看试题解析
9. 定义在R上的偶函数 $f (x)$ 满足 $f (x) = f (2 - x)$ ，且当 $x \in [0 ， 1]$ 时， $f (x) = e^{x} - 1$ ，若关于x的方程 $f (x) = m (x + 1) (m > 0)$ 恰有5个解，则m的取值范围为（）

A、 $(\frac{e - 1}{6} ， \frac{e - 1}{5})$ B、 $(\frac{e - 1}{6} ， \frac{e - 1}{4})$ C、 $(\frac{e - 1}{8} ， \frac{e - 1}{6})$ D、 $(0 ， e - 1)$

查看试题解析
10. 已知抛物线 $C ： y^{2} = 4 x$ ， O为坐标原点.若存在过点 $M (m ， 0) (m > 0)$ 的直线l与C相交于A､B两点，且 $| A M | \cdot | M B | = | O M |^{2}$ ，则实数m的取值范围为（）

A、 $[4 ， + \infty)$ B、 $(0 ， 4)$ C、 $[\frac{4}{3} ， + \infty)$ D、 $(0 ， \frac{4}{3})$

查看试题解析
11. 函数f（x）=lnx+e^x（e为自然对数的底数）的零点所在的区间是（）

A、 $(0 ， \frac{1}{e})$ B、 $(\frac{1}{e} ， 1)$ C、（1，e） D、（e，+∞）

查看试题解析

二、填空题

12. 已知 $a > 0$ ，函数 $f (x) = {\begin{matrix} x^{2} + 2 a x + a ， x \leq 0 ， \\ - x^{2} + 2 a x - 2 a ， x > 0. \end{matrix}$ 若关于 $x$ 的方程 $f (x) = a x$ 恰有2个互异的实数解，则 $a$ 的取值范围是.

查看试题解析
13. 设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）= ${\begin{matrix} x^{2} ， x \in D \\ x ， x \notin D \end{matrix}$ ，其中集合D={x|x= $\frac{n - 1}{n}$ ，n∈N^*}，则方程f（x）﹣lgx=0的解的个数是．

查看试题解析
14. 已知函数f（x）=|x²+3x|，x∈R，若方程f（x）﹣a|x﹣1|=0恰有4个互异的实数根，则实数a的取值范围为．

查看试题解析
15. 牛顿选代法又称牛顿—拉夫逊方法，它是牛顿在17世纪提出的一种在实数集上近似求解方程根的一种方法．具体步骤如下：设 $r$ 是函数 $y ＝ f (x)$ 的一个零点，任意选取 $x_{0}$ 作为 $r$ 的初始近似值，过点 $(x_{0}, f (x_{0}))$ 作曲线 $y ＝ f (x)$ 的切线 $l_{1}$ ，设 $l_{1}$ 与 $x$ 轴交点的横坐标为 $x_{1}$ ，并称 $x_{1}$ 为 $r$ 的1次近似值；过点 $(x_{1} ， f (x_{1}))$ 作曲线 $y ＝ f (x)$ 的切线 $l_{2}$ ，设 $l_{2}$ 与 $x$ 轴交点的横坐标为 $x_{2}$ ，称 $x_{2}$ 为 $r$ 的2次近似值．一般的，过点 $(x_{n}, f (x_{n})) (n \in N)$ 作曲线 $y ＝ f (x)$ 的切线 $l_{n +}_{1}$ ，记 $l_{n +}_{1}$ 与 $x$ 轴交点的横坐标为 $x_{n +}_{1}$ ，并称 $x_{n +}_{1}$ 为 $r$ 的 $n + 1$ 次近似值．设 $f (x) = x^{3} + x - 1$ $(x \geq 0)$ 的零点为 $r$ ，取 $x_{0} ＝ 0$ ，则 $r$ 的 $2$ 次近似值为；设 $a_{n} = \frac{3 x_{n}^{3} + x_{n}}{2 x_{n}^{3} + 1}$ ， $n \in N^{*},$ 数列 ${a_{n}}$ 的前 $n$ 项积为 $T_{n}$ ．若任意 $n \in N^{*}, T_{n} < λ$ 恒成立，则整数 $λ$ 的最小值为．

查看试题解析
16. 已知函数f（x）= $\frac{1}{x} - 2^{x}$ ，则 $f (\frac{1}{2})$ f（1）（填“＞”或“＜”）；f（x）在区间 $(\frac{n - 1}{n} ， \frac{n}{n + 1})$ 上存在零点，则正整数n= ．

查看试题解析
17. 若 $ω$ 为方程 $x^{3} = 2$ 的一个虚根，则方程 $x^{3} = 1$ 的一个虚根为.（用 $ω$ 表示）.

查看试题解析
18. 方程 $x^{3} - 6 x^{2} + 9 x - 10 = 0$ 的实根个数是．

查看试题解析
19. 设 $a ， b > 0$ ，满足：关于x的方程 $\sqrt{| x |} + \sqrt{| x + a |} = b$ 恰有三个不同的实数解 $x_{1} ， x_{2} ， x_{3}$ ，且 $x_{1} < x_{2} < x_{3} = b$ ，则 $a + b$ 的值为．

查看试题解析
20. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，当 $x > 0$ 时， $f (x) = {\begin{array}{l} 2^{| x - 1 |} - 1 ， 0 < x \leq 2 \\ \frac{1}{2} f (x - 2) ， x > 2 \end{array}$ 有下列结论：
①函数 $f (x)$ 在 $(- 6 ， - 5)$ 上单调递增；

②函数 $f (x)$ 的图象与直线 $y = x$ 有且仅有2个不同的交点；

③若关于 $x$ 的方程 ${[f (x)]}^{2} - (a + 1) f (x) + a = 0 (a \in R)$ 恰有4个不相等的实数根，则这4个实数根之和为8；

④记函数 $f (x)$ 在 $[2 k - 1 ， 2 k] (k \in N^{*})$ 上的最大值为 $a_{k}$ ，则数列 ${a_{n}}$ 的前 $7$ 项和为 $\frac{127}{64}$ .

其中所有正确结论的编号是.

查看试题解析
21. 已知 $f (x) = \frac{{(\ln x + 1)}^{2}}{x}$ ， $g (x) = a (\ln x + 1) - \frac{1}{2} x$ ，若方程 $f (x) = g (x)$ 有四个不等实根，则a的取值范围为.

查看试题解析
22. 定义关于 $x$ 的曲线 $f (a, b, c) = a x^{2} + b x + c$ ，则与曲线 $f (1, 2, 0)$ 和 $f (- 1, 2, 0)$ 都相切的直线 $l$ 的方程为， $F (x) = {\begin{array}{l} f (- 1, 2 a, - 2 a), x > 0 \\ f (1, 2 a, a), x \leq 0 \end{array}$ ，已知 $a > 0$ ，若关于 $x$ 的方程 $F (x) = f (0, a, 0)$ 有三个不同的实根，则 $a =$ .

查看试题解析
23. 设函数 $f (x) = | x - a | - \frac{2}{x} + a$ ，若关于 $x$ 的方程 $f (x) = 1$ 有且仅有两个不同的实数根，则实数 $a$ 的取值构成的集合为．

查看试题解析
24. 已知函数 $f (x) = | e^{| x |} - 2 |$ ，关于x的方程 ${[f (x)]}^{2} + b f (x) + b^{2} - 1 = 0$ 恰有5个不同实数解，则实数 $b =$ .

查看试题解析

三、解答题

25. 已知函数f(x)=sinx-ln(1+x)，f’(x)为f(x)的导数。证明：

(1)、f’(x)在区间(-1， $\frac{π}{2}$ )存在唯一极大值点；

(2)、f(x)有且仅有2个零点。

查看试题解析
26. 已知函数 $f (x) = \ln x + \frac{a}{x}$ ， $a \in R$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若经过坐标原点恰好可作两条直线与曲线 $y = f (x)$ 相切，求a的取值范围.

查看试题解析
27. 已知双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两条渐近线分别为 $l_{1} ： y = 2 x$ ， $l_{2} ： y = － 2 x$ .

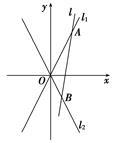(1)、求双曲线E的离心率；

(2)、如图，O为坐标原点，动直线l分别交直线 $l_{1}$ ， $l_{2}$ 于A，B两点（A，B分别在第一、四象限），且 $△ O A B$ 的面积恒为8.试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程；若不存在，说明理由.

查看试题解析
28. 已知函数 $f (x) = 2 a \ln x + \frac{1}{x^{2}} (a \in R)$

(1)、当 $a = 1$ 时，求证：函数 $f (x)$ 没有零点；

(2)、若存在两个不相等正实数 $x_{1}$ ， $x_{2}$ ，满足 $f (x_{1}) = f (x_{2})$ ，且 $x_{1} x_{2} = 1$ ，求实数a的取值范围．

查看试题解析
29. 已知函数 $f (x) = \frac{1}{3} x^{3} + a x^{2} + b x + 1$ （a， $b \in R$ ）.

(1)、若 $b = 0$ ，且 $f (x)$ 在 $(0 ， + \infty)$ 内有且只有一个零点，求a的值；

(2)、若 $a^{2} + b = 0$ ，且 $f (x)$ 有三个不同零点，问是否存在实数a使得这三个零点成等差数列？若存在，求出a的值，若不存在，请说明理由；

(3)、若 $a = 1$ ， $b < 0$ ，试讨论是否存在 $x_{0} \in (0 ， \frac{1}{2}) \cup (\frac{1}{2} ， 1)$ ，使得 $f (x_{0}) = f (\frac{1}{2})$ .

查看试题解析
30. 已知函数 $f (x) = \frac{1}{2} x^{2} - (a + 1) x + a ln x$ .

(1)、当 $a > 1$ 时，求 $f (x)$ 的单调区间；

(2)、当 $a < 1$ 且 $a \neq 0$ 时，若 $f (x)$ 有两个零点，求 $a$ 的取值范围.

查看试题解析
31. 设函数 $f (x) = | x - 1 | + | | x | - 1 |$ .

(1)、画出 $y = f (x)$ 的图象；

(2)、若过点 $A (2 ， 0)$ 的直线 $l$ 与 $y = f (x)$ 的图象恰有4个交点，求 $l$ 斜率的取值范围.

查看试题解析
32. 已知函数 $f (x) = x^{3} - \frac{3}{2} a x^{2} (a > 0)$ .

(1)、若函数 $h (x) = \frac{f (x) \cdot e^{x}}{x}$ 在 $(0, 1)$ 上单调递减，求 $a$ 的取值范围；

(2)、若过点 $(a, b)$ 可作曲线 $f (x)$ 的三条切线，证明： $- \frac{5}{8} a^{3} < b < f (a)$ .

查看试题解析
33. 设函数 $f (x) = \frac{x}{e^{2 x}} + c (e = 2.71828 \dots ， c \in R)$ ．

(1)、求f（x）的单调区间及最大值；

(2)、讨论关于x的方程|lnx|=f（x）根的个数．

查看试题解析
34. 已知函数f（x）=（1﹣m）lnx+ $\frac{m}{2} x^{2}$ ﹣x，m∈R且m≠0．
（Ⅰ）当m=2时，令g（x）=f（x）+log₂（3k﹣1），k为常数，求函数y=g（x）的零点的个数；
（Ⅱ）若不等式f（x）＞1﹣ $\frac{1}{m}$ 在x∈[1，+∞）上恒成立，求实数m的取值范围．

查看试题解析
35. 已知函数 $f (x) = cos 2 x ， g (x) = sin x$

(1)、是否存在 $x_{0} \in (\frac{π}{6} ， \frac{π}{4})$ ，使得 $f (x_{0}) ， g (x_{0}) ， f (x_{0}) \cdot g (x_{0})$ ，按照某种顺序成等差数列？若存在，请确定 $x_{0}$ 的个数；若不存在，请说明理由；

(2)、求实数 $a$ 与正整数 $n$ ，使得 $F (x) = f (x) + a g (x)$ 在 $(0 ， n π)$ 内恰有 $2019$ 个零点.

查看试题解析