【备考2024】高考数学(三角函数版块)细点逐一突破训练:弦切互化
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 若点 在直线 上,则 的值等于( )A、 B、 C、 D、2. 已知 ,且 ,则 ( )A、
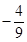 B、
B、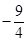 C、
D、
3. 若 ,则 ( )
C、
D、
3. 若 ,则 ( )
A、 B、1 C、 D、4. 已知cosα=﹣ ,且α∈( ,π),则tan(α+ )等于( )A、﹣ B、﹣7 C、 D、75. 已知 , 则( )A、 B、 C、3 D、6. 若 , 则( )A、 B、 C、 D、7. 下列命题正确的是( )A、 B、函数的最小正周期是 C、 , 则 D、若 , 则8. 下列等式成立的有( )A、 B、 C、 D、9. 已知 , 则的值为( )A、 B、 C、 D、10. 已知 , 则( )A、 B、 C、 D、11. 在中,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件12. 已知 , 则( )A、 B、 C、 D、13. 在锐角 中,已知 ,则下列正确的结论为( )A、 B、 C、 D、二、填空题
-
14. 若 , 为钝角,则 的值为(用 表示).15. 已知 ,则tanα= .16. 已知sinθ=cosθ,则tanθ的值为。17. 如图,已知向量满足: , 且.若则.
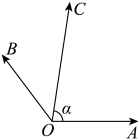 18. 若 , , 则 .19. 已知tanα=3,π<α , 则cosα﹣sinα= .20. 若正数满足 , 且 , 则的值为.21. 已知 , 则.22. 已知函数是偶函数,则 .23. 已知 , 则的值为.24. 已知 , 则的值为 .25. 在中,内角所对的边分别是 , 且 , 点是线段的中点,若 , 则面积的最大值是.26. .
18. 若 , , 则 .19. 已知tanα=3,π<α , 则cosα﹣sinα= .20. 若正数满足 , 且 , 则的值为.21. 已知 , 则.22. 已知函数是偶函数,则 .23. 已知 , 则的值为.24. 已知 , 则的值为 .25. 在中,内角所对的边分别是 , 且 , 点是线段的中点,若 , 则面积的最大值是.26. .三、解答题