华师大版数学八年级上册12.2 整式的乘法同步练习（提升卷）

试卷更新日期：2023-08-18 类型：同步测试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、m+m=m² B、(-3x)²=6x² C、(m+2n)²=m²+4n² D、(m+3)(m-3)=m²-9

查看试题解析
2. 已知 $(x - 4) (x - 9) = x^{2} + m x + 36$ ，则m的值为（）

A、 $- 13$ B、13 C、 $- 5$ D、5

查看试题解析
3. 若多项式 $x^{2} + b x + c$ 因式分解的结果为 $(x - 2) (x + 3)$ ，则 $b + c$ 的值为（）

A、 $- 5$ B、 $- 1$ C、5 D、6

查看试题解析
4. 若多项式 $2 x^{2} + a x - 6$ 能分解成两个一次因式的积，且其中一个次因式 $2 x - 3$ ，则 $a$ 的值为（）

A、1 B、5 C、-1 D、-5

查看试题解析
5. 如图，根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后制成的长方形铁皮（阴影部分）的面积是多少？几名同学经过讨论给出了不同的答案，其中正确的是（）
①（x-5）（x-6）；②x²-5x-6（x-5）；③x²-6x-5x；④x²-6x-5（x-6）

A、①②④ B、①②③④ C、① D、②④

查看试题解析
6. 已知 $(x - 2) (x^{2} + m x + n)$ 的乘积项中不含 $x^{2}$ 和 $x$ 项，则 $m ， n$ 为（）

A、 $m = 2 ， n = 4$ B、 $m = 3 ， n = 6$ C、 $m = - 2 ， n = - 4$ D、 $m = - 3 ， n = - 6$

查看试题解析
7. 计算（　　） $\div \frac{1}{2} a b^{2} = 8 a$ ，正确的结果是（　　）

A、16 $a^{2} b^{2}$ B、4 $a b$ ² C、 $(4 a b)^{2}$ D、 $(2 a b)^{2}$

查看试题解析
8. 若 $(2 x - 3) (x + 2) = 2 x^{2} + m x + n$ ，则m与n的值分别是（　　）

A、 $- 1 ， 6$ B、1 $， - 6$ C、 $- 3 ， - 2$ D、 $- 3 ， 2$

查看试题解析
9. 如果 $(2 n x + 3 x^{2} + m x^{3}) (- 4 x^{2})$ 的结果中不含x的五次项，那么m的值为（）

A、1 B、0 C、-1 D、 $- \frac{1}{4}$

查看试题解析
10. 下列计算正确的是（）

A、 $2 a \cdot 3 b^{2} = 5 a b^{2}$ B、 $a^{4} \div a^{2} + a^{2} = 2 a^{2}$ C、 ${(- 3 a^{2} b)}^{2} = 6 a^{4} b^{2}$ D、 $a^{3} \cdot a^{4} = a^{12}$

查看试题解析

二、填空题

11. 计算： $3 a^{2} b · (- 2 a b^{2}) =$ .

查看试题解析
12. 若 $(x + 3) (x + m) = x^{2} - 2 x - 15$ ．则m＝．

查看试题解析
13. 观察图，写出此图可以验证的一个等式．（写出一个即可）

查看试题解析
14. 把多项式x²﹣6x＋m分解因式得（x＋3）（x﹣n），则m＋n的值是．

查看试题解析
15. 计算： $3 a^{3} \cdot 2 a$ ＋ $a^{6}$ ÷ $a^{2}$ ＝．

查看试题解析

三、综合题

16. 甲乙两人共同计算一道整式乘法题 $(2 x + a) (3 x + b)$ .甲由于把第一个多项式中的“ $+ a$ ”看成了“ $- a$ ”，得到的结果为 $6 x^{2} + 11 x - 10$ .乙由于漏抄了第二个多项式中 $x$ 的系数，得到的结果为 $2 x^{2} - 9 x + 10$ .

(1)、求正确的 $a$ 、 $b$ 的值；

(2)、计算出这道整式乘法题的正确结果.

查看试题解析
17. 探究：我们小学时学过乘法分配律a（b+c）＝ab+ac.

下面我们用等积法证明乘法分配律：

如图，方法一：长方形ABCD的一边长为a，另一边长为（b+c），所以长方形ABCD的面积为a（b+c）；

方法二，长方形ABFE的面积为ab，长方形CDEF的面积为ac，所以长方形ABCD的面积为（ab+ac），所以a（b+c）＝ab+ac.

我们把这种用两种不同的方式表示同一图形面积的方法称为等积法.

(1)、应用
请你用等积法，画出图形，并仿照上面的说理方法证明：（a+b）（c+d）＝ac+ad+bc+bd；

(2)、拓展
请直接写出（a+b）（c+d+e）＝.

查看试题解析
18. 在“整式乘法与因式分解”这一章的学习过程中，我们常采用构造几何图形的方法对代数式的变形加以说明．例如，利用图 $1$ 中边长分别为a，b的正方形，以及长为a，宽为b的长方形卡片若干张拼成图2（卡片间不重叠、无缝隙），可以用来解释完全平方公式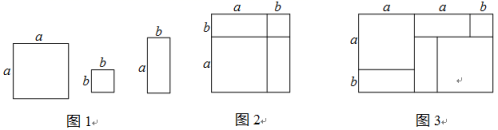： $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ．
请你解答下面的问题：

(1)、利用图1中的三种卡片若干张拼成图 $3$ ，可以解释等式：；

(2)、利用图1中三种卡片若干张拼出一个面积为 $2 a^{2} + 5 a b + 2 b^{2}$ 的长方形ABCD，请你分析这个长方形的长和宽．

查看试题解析
19. 芳芳计算一道整式乘法的题：(2x +m)(5x-4)，由于芳芳将第一个多项式中的“+ m”抄成“-m”，得到的结果为10x² - 33x + 20．

(1)、求m的值；

(2)、请解出这道题的符合题意结果．

查看试题解析
20. 某小区有一块长为（ $3 a + b$ ）米，宽为（ $2 a + b$ ）米的长方形地块（如图所示），物业公司计划将中间修建一小型喷泉，然后将周围（阴影部分）进行绿化；

(1)、应绿化的面积是多少平方米?

(2)、当 $a = 3 ， b = 2$ 时求出应绿化的面积.

查看试题解析

华师大版数学八年级上册12.2 整式的乘法 同步练习（提升卷）

一、选择题

二、填空题

三、综合题

华师大版数学八年级上册12.2 整式的乘法同步练习（提升卷）