【备考2024】高考数学（三角函数版块）细点逐一突破训练：三角函数的化简求值

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 设α∈（0， $\frac{π}{2}$ ），β∈（0， $\frac{π}{2}$ ），且tanα= $\frac{1 + \sin β}{\cos β}$ ，则（）

A、3α﹣β= $\frac{π}{2}$ B、3α+β= $\frac{π}{2}$ C、2α﹣β= $\frac{π}{2}$ D、2α+β= $\frac{π}{2}$

查看试题解析
2. 已知角 $α$ 满足 $t a n (α - \frac{π}{4}) = \frac{1}{3}$ ，则 $s i n 2 α =$ （）

A、 $\frac{4}{5}$ B、 $- \frac{4}{5}$ C、 $- \frac{7}{9}$ D、 $\frac{4}{9}$

查看试题解析
3. 瑞士数学家欧拉发现了复指数函数和三角函数的关系，并写下 $e^{i θ} = c o s θ + i s i n θ$ ，被誉为“数学中的天桥”，据此 ${(c o s \frac{π}{6} + i s i n \frac{π}{6})}^{6} =$ （）

A、1 B、-1 C、0 D、-i

查看试题解析
4. 设 $s i n 20 ° = m$ ， $c o s 20 ° = n$ ，化简 $\frac{1 + t a n 10 °}{1 - t a n 10 °} - \frac{2 c o s 70 °}{c o s 50 °} =$ （）

A、 $\frac{n}{m}$ B、 $- \frac{m}{n}$ C、 $\frac{m}{n}$ D、 $- \frac{n}{m}$

查看试题解析
5. 已知 $△ A B C$ 为锐角三角形，且 $s i n A = s i n B s i n C$ ，则下列结论中正确的是（）

A、 $t a n B + t a n C = t a n B t a n C$ B、 $t a n A t a n B t a n C = t a n A + t a n B + t a n C$ C、 $1 < t a n A \leq \frac{4}{3}$ D、 $t a n A t a n B t a n C$ 的最小值为4

查看试题解析
6. 已知 $α \in (- \frac{π}{2} ， \frac{π}{2})$ ，且 $3 \cos 2 α + 8 \sin α + 5 = 0$ ，则 $\cos α =$ （）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{2}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析
7. 若 $x \in (0 ， 1) ， a = \frac{\tan x}{x} ， b = \frac{\tan (x^{2})}{x^{2}} ， c = {(\frac{\tan x}{x})}^{2}$ ，则 $a ， b ， c$ 的大小关系是（）

A、 $a > b > c$ B、 $b > a > c$ C、 $b > c > a$ D、 $c > a > b$

查看试题解析
8. 已知 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 是圆 $x^{2} + y^{2} = 4$ 上两个不同的点，且满足 $x_{1} x_{2} + y_{1} y_{2} = 2$ ，则 $| x_{1} + y_{1} - 8 | + | x_{2} + y_{2} - 8 |$ 的最大值为（）

A、 $2 \sqrt{3} + 8 \sqrt{2}$ B、 $8 + \sqrt{6}$ C、 $4 \sqrt{3} + 16 \sqrt{2}$ D、 $16 + 2 \sqrt{6}$

查看试题解析
9. 已知 $A (x_{A}, y_{A})$ 是圆心为坐标原点O，半径为1的圆上的任意一点，将射线OA绕点 $O$ 逆时针旋转 $\frac{2 π}{3}$ 到OB交圆于点 $B (x_{B}, y_{B})$ ，则 $2 y_{A} + y_{B}$ 的最大值为（）

A、3 B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
10. 已知锐角 $α$ 满足 $cos (α + \frac{π}{6}) = \frac{3}{5}$ ，则 $sin (2 α + \frac{π}{3}) =$ （）

A、 $\frac{12}{25}$ B、 $\pm \frac{12}{25}$ C、 $\frac{24}{25}$ D、 $\pm \frac{24}{25}$

查看试题解析
11. 已知 $tan (θ + \frac{π}{4}) = 3$ ，则 $cos (2 θ - \frac{π}{4}) =$ （）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{\sqrt{2}}{10}$ D、 $\frac{7 \sqrt{2}}{10}$

查看试题解析

二、填空题

12. 已知 $\frac{\tan α}{\tan (α + \frac{π}{4})} = - \frac{2}{3}$ ，则 $\sin (2 α + \frac{π}{4})$ 的值是.

查看试题解析
13. 设a₁、a₂∈R，且 $\frac{1}{2 + s i n α_{1}}$ + $\frac{1}{2 + s i n (2 α_{2})}$ =2，则|10π﹣α₁﹣α₂|的最小值等于．

查看试题解析
14. 已知 $| \vec{a} + 2 \vec{b} | = | \vec{a} | = 2$ ，则 $| \vec{a} + \vec{b} | + | 2 \vec{b} |$ 的取值范围是．

查看试题解析
15. 若函数 $f (x) = \sin 2 x + \cos 2 x$ 在 $[0 ， \frac{m}{2}]$ 和 $[3 m ， π]$ 上均单调递增，则实数m的取值范围为．

查看试题解析
16. 若 $2 cos 2 α = sin (\frac{π}{4} - α)$ ， $α \in (\frac{π}{2}, π)$ ，则 $sin 2 α =$ ．

查看试题解析
17. 化简 $\frac{1}{sin 70 °} - \frac{\sqrt{3}}{cos 70 °}$

查看试题解析
18. 已知 $sin α = - \frac{3}{5}$ ，且 $α$ 是第三象限的角，则 $tan 2 α$ 的值为．

查看试题解析
19. 若sinθ=﹣ $\frac{1}{3}$ ，tanθ＞0，则cosθ= ， tan2θ= ．

查看试题解析
20. 已知sinθ+cosθ= $\frac{1}{5}$ ，θ∈（0，π），则 $\frac{c o s^{2} θ + 2 s i n^{2} θ}{3 c o s^{2} θ - 4 s i n^{2} θ}$ 的值是．

查看试题解析
21. 设当x=α时，函数f（x）=3sinx+cosx取得最大值，则tan2α= ．

查看试题解析

三、解答题

22. 已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（ $- \frac{3}{5} ， - \frac{4}{5}$ ）．
（Ⅰ）求sin（α+π）的值；
（Ⅱ）若角β满足sin（α+β）= $\frac{5}{13}$ ，求cosβ的值．

查看试题解析
23. 设常数 $a \in R$ ，函数 $f （ x ）$ $= a s i n 2 x + 2 c o s^{2} x$

(1)、若 $f （ x ）$ 为偶函数，求 $a$ 的值；

(2)、若 $f 〔 \frac{π}{4} 〕$ $= \sqrt{3} + 1$ ，求方程 $f （ x ） = 1 - \sqrt{2}$ 在区间 $［ - π ， π ］$ 上的解。

查看试题解析
24. 已知函数f（x）=sin²x﹣cos²x﹣2 $\sqrt{3}$ sinx cosx（x∈R）．
（Ⅰ）求f（ $\frac{2 π}{3}$ ）的值．
（Ⅱ）求f（x）的最小正周期及单调递增区间．

查看试题解析
25. 函数f（x）=6cos² $\frac{ω x}{2} + \sqrt{3}$ sinωx﹣3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．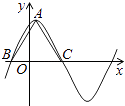

(1)、求ω的值及函数f（x）的值域；

(2)、若f（x₀）= $\frac{8 \sqrt{3}}{5}$ ，且x₀∈（﹣ $\frac{10}{3} ， \frac{2}{3}$ ），求f（x₀+1）的值．

查看试题解析
26. 在直线坐标系xOy中，曲线C₁： ${\begin{matrix} x = t c o s α \\ y = t s i n α \end{matrix}$ (t为参数，t≠0)其中 $0 \leq α \leq π$ .在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C₂：ρ＝2sinθ，C₃：ρ＝2 $\sqrt{3}$ cosθ.

(1)、求C₂与C₃交点的直角坐标；

(2)、若C₁与C₂相交于点A，C₁与C₃相交于点B，求|AB|的最大值．

查看试题解析
27. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $\sqrt{3} c \sin B = a + \sqrt{3} \frac{b \cos C}{\tan B}$ .

(1)、若 $B = \frac{π}{4}$ ， $c = \sqrt{6} + \sqrt{2}$ ，求 $△ A B C$ 的面积；

(2)、若 ${(\frac{a}{c})}^{2} + 6 \cos 2 B = 6$ ，求角 $C$ .

查看试题解析
28. 函数 $f (x) = sin (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的部分图像如图所示，将 $y = f (x)$ 的图象向右平移 $\frac{π}{4}$ 个单位长度后得到函数 $y = g (x)$ 的图象．

(1)、求函数 $y = g (x)$ 的解折式；

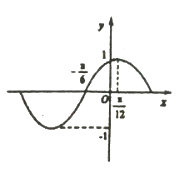(2)、在 $Δ A B C$ 中，角 $A ， B ， C$ 满足 $2 {sin}^{2} \frac{A + B}{2} = g (C + \frac{π}{3}) + 1$ ，且其外接圆的半径 $R = 2$ ，求 $Δ A B C$ 的面积的最大值．

查看试题解析
29. 如图，在平面直角坐标系xOy中，以x轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A，B两点，x轴正半轴与单位圆交于点M，已知 $S_{△ O A M} = \frac{\sqrt{5}}{5}$ ，点B的纵坐标是 $\frac{\sqrt{2}}{10}$ ，
（Ⅰ）求cos（α﹣β）的值；
（Ⅱ）求2α﹣β 的值．

查看试题解析
30. 已知函数f（x）=2sinxsin（ $\frac{π}{6}$ ﹣x）．
（Ⅰ）求f（ $\frac{π}{3}$ ）及f（x）的最小正周期T的值；
（Ⅱ）求f（x）在区间[﹣ $\frac{π}{6}$ ， $\frac{π}{4}$ ]上的最大值和最小值．

查看试题解析
31. 已知sin（α+ $\frac{π}{4}$ ）= $\frac{\sqrt{2}}{10}$ ，α∈（ $\frac{π}{2}$ ，π）．求：

(1)、cosα的值；

(2)、sin（2α﹣ $\frac{π}{4}$ ）的值．

查看试题解析
32. 已知函数f（x）= $\sqrt{3}$ sinxcosx+cos²x
（I）求函数f（x）的最小正周期；
（II）若﹣ $\frac{π}{2}$ ＜α＜0，f（α）= $\frac{5}{6}$ ，求sin2α的值．

查看试题解析
33. 已知f（α）=cosα $f (α) = \cos α \sqrt{\frac{1 - \sin α}{1 + \cos α}} + \sin α \sqrt{\frac{1 - \cos α}{1 + \cos α}}$

（Ⅰ）当α为第二象限角时，化简f（α）；
（Ⅱ）当α∈（ $\frac{π}{2}$ ，π）时，求f（α）的最大值．

查看试题解析
34. 已知 $\vec{m}$ =（cosα，sinα）， $\vec{n}$ =（ $\sqrt{3}$ ，﹣1），α∈（0，π）．

(1)、若 $\vec{m}$ ⊥ $\vec{n}$ ，求角α的值；

(2)、求| $\vec{m}$ + $\vec{n}$ |的最小值．

查看试题解析
35. 已知角α终边逆时针旋转 $\frac{π}{6}$ 与单位圆交于点 $(\frac{3 \sqrt{10}}{10} ， \frac{\sqrt{10}}{10})$ ，且 $\tan (α + β) = \frac{2}{5}$ ．

(1)、求 $\sin (2 α + \frac{π}{6})$ 的值，

(2)、求 $\tan (2 β - \frac{π}{3})$ 的值．

查看试题解析