陕西省榆林市榆阳区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 观察下列图形,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列各式中错误的是( )A、 B、 C、 D、3. 在中, , 则的度数是( )A、 B、 C、 D、4. 下列各式从左到右的变形,是因式分解的为( )A、 B、 C、 D、5. 已知关于x的方程 有增根,则a的值为( )A、4 B、5 C、6 D、﹣56. 如图,在中, , 点 , 于点 , 于点 , , 则( )
2. 若 , 则下列各式中错误的是( )A、 B、 C、 D、3. 在中, , 则的度数是( )A、 B、 C、 D、4. 下列各式从左到右的变形,是因式分解的为( )A、 B、 C、 D、5. 已知关于x的方程 有增根,则a的值为( )A、4 B、5 C、6 D、﹣56. 如图,在中, , 点 , 于点 , 于点 , , 则( ) A、 B、 C、 D、7. 如图,下列条件不能判定四边形是平行四边形的是( )
A、 B、 C、 D、7. 如图,下列条件不能判定四边形是平行四边形的是( )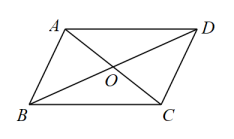 A、 , B、 , C、 , D、 ,8. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( )
A、 , B、 , C、 , D、 ,8. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 若分式有意义,则实数的取值范围是 .10. 多项式6a2b-3ab2的公因式是11. 已知一个正n边形的每个内角都为120°,则 .12. “孔子周游列国”是流传很广的故事.有一次他和学生到离他们住的驿站30里的书院参观,学生步行出发1小时后,孔子坐牛车出发,牛车的速度是步行的1.5倍,孔子和学生们同时到达书院,设学生步行的速度为每小时x里,则可列方程为 .13. 如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,且AB=1,BC=2,则AD的值为.

三、解答题
-
14. 因式分解: .15. 解分式方程: .16. 如图,在△ABC中,AB>AC,请用尺规作图法,在BC边上求作一点P,使得AP=PB.(保留作图痕迹,不写作法)
 17. 如图,在中,点E、F分别为上的点,连接 , 且 .求证: .
17. 如图,在中,点E、F分别为上的点,连接 , 且 .求证: . 18. 解不等式组:并把解集在如图所示的数轴上表示出来.
18. 解不等式组:并把解集在如图所示的数轴上表示出来. 19. 如图,在四边形中,、、分别是、、的中点, . 求证: .
19. 如图,在四边形中,、、分别是、、的中点, . 求证: . 20. 已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB, CE∥AD.问:△CDE是否为等腰三角形?为什么?
20. 已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB, CE∥AD.问:△CDE是否为等腰三角形?为什么? 21. 如图,已知的三个顶点的坐标分别为、、 .
21. 如图,已知的三个顶点的坐标分别为、、 .
⑴将先向左平移4个单位,再向上平移1个单位得到 , 在图中画出;
⑵在图中作出关于原点成中心对称的 .
22. 先化简 , 再从 , , 中选择一个适当的数代入求值.23. 如图,在中, , , 是的垂直平分线,交、于点、连接、 . 求证: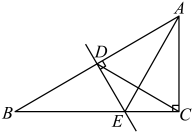 (1)、是等边三角形;(2)、点在线段的垂直平分线上.24. “我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法,配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.例如:
(1)、是等边三角形;(2)、点在线段的垂直平分线上.24. “我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法,配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.例如:
分解因式: .
求代数式的最小值: .
∵ , ∴ , ∴当时,有最小值,最小值是 .
根据材料用配方法解决下列问题:
(1)、分解因式:;(2)、当为何值时,多项式有最大值?并求出这个最大值.
