江苏省泰州市兴化市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列校徽主体图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{8}$

查看试题解析
3. $⊙ O$ 的半径为5，圆心O到直线l的距离为3，则直线l与 $⊙ O$ 的位置关系是 $($ $)$

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
4. 将分式 $\frac{a b}{a - b}$ 中的 $a$ 、 $b$ 都扩大到3倍，则分式的值（）

A、不变 B、扩大3倍 C、扩大9倍 D、扩大6倍

查看试题解析
5. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
6. 点 $I$ 是 $△ A B C$ 的外心，则点 $I$ 是 $△ A B C$ 的（）

A、三条垂直平分线交点 B、三条角平分线交点 C、三条中线交点 D、三条高的交点

查看试题解析

二、填空题

7. 若分式 $\frac{2}{x + 3}$ 无意义，则 $x =$ ．

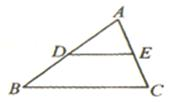
查看试题解析
8. 若二次根式 $\sqrt{5 - 2 x}$ 在实数范围内有意义，则x的取值范围为．

查看试题解析
9. 设x₁ ， x₂是一元二次方程x²-3x-2=0的两个实数根，则x₁+x₂= ．

查看试题解析
10. 直角三角形的两直角边分别3，4；则它的外接圆半径R= ．

查看试题解析
11. 如图，在△ABC中，D、E分别是边AB、AC的中点，BC=8，则DE= ．

查看试题解析
12. 已知反比例函数 $y = \frac{m + 5}{x}$ 的图像在二、四象限，则 $m$ 的取值范围是．

查看试题解析
13. 若a是方程 $x^{2} - 2 x - 1 = 0$ 的解，则代数式 $2 a^{2} - 4 a + 2022$ 的值为．

查看试题解析
14. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E$ ， $C E = \sqrt{3}$ ， $B E = 1$ ，则 $O C =$ ．

查看试题解析
15. 某农场去年种植西瓜5亩，总产量为 $10000 k g$ ．今年该农场扩大了种植面积，并引进新品种，使总产量增长到 $30000 k g$ ．已知种植面积的增长率是平均亩产量增长率的2倍，则平均亩产量的增长率为．

查看试题解析
16. 如图，点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $F$ 在网格中的格点处， $A F$ 与 $B C$ 相交于点 $E$ ，设小正方形的边长为1，则阴影部分 $△ D E F$ 的面积等于．

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{x - 2}{x^{2}} \div (1 - \frac{2}{x})$ ；

(2)、 $\sqrt{18} - \sqrt{8} + \sqrt{\frac{1}{2}}$ ．

查看试题解析
18. 解方程：

(1)、 $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$ ；

(2)、 $x^{2} + 3 x - 2 = 0$ ．（用配方法）

查看试题解析
19. 先化简，再求值 $\frac{3 - a}{2 a - 4} \div (a + 2 - \frac{5}{a - 2})$ ，其中 $a = \sqrt{3} - 3$

查看试题解析
20. 如图为某新款茶吧机，开机加热时每分钟上升20℃，加热到100℃时，停止加热，水温开始下降，此时水温 $y$ （℃）与通电时间 $x (m i n)$ 成反比例关系．当水温降至20℃时，饮水机再自动加热，若水温在20℃时接通电源，水温 $y$ 与通电时间 $x$ 之间的关系如图所示．

(1)、水温从20℃加热到100℃，需要分钟；

(2)、在水温下降过程中，请求出反比例函数表达式；

(3)、求在一个加热周期内水温不低于40℃的时间范围？

查看试题解析
21. 如图，已知矩形 $A B C D$ ，点 $P$ 是边 $A B$ 边上一点．

(1)、如图1，将矩形 $A B C D$ 沿着直线 $C P$ 翻折，点 $B$ 恰好落在 $A D$ 上，其对称点记为点 $B^{'}$ ， $A B = 4$ ， $B C = 5$ ，求 $A P$ 长；

(2)、如图2，请利用圆规和无刻度直尺在边 $A D$ 上找一点 $H$ ，使得 $∠ C P H = 60 °$ ．（在图中标明相应字母，保留作图痕迹，不写作法）

查看试题解析
22. 如图，一次函数 $y_{1} = k x + b$ 与反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图象交于 $A (1 ， 4)$ 、 $B (2 ， 2)$ 两点．

(1)、分别求出该一次函数和反比例函数的表达式；

(2)、取 $A B$ 中点 $E$ ，连接 $O E$ ，则 $△ O E C$ 是等腰三角形吗？如是，请证明；如不是，请说明理由．

查看试题解析
23. 端午节前夕，某超市从厂家分两次购进蛋黄粽子、红豆粽子，两次进货时，两种粽子的进价不变．第一次购进蛋黄粽子60袋和红豆粽子90袋，总费用为4800元；第二次购进蛋黄粽子40袋和红豆粽子80袋，总费用为3600元．

(1)、求蛋黄粽子、红豆粽子每袋的进价各是多少元？

(2)、当蛋黄粽子销售价为每袋70元时；每天可售出20袋，为了促销，该超市决定对蛋黄粽子进行降价销售．经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当蛋黄粽子每袋的销售价为多少元时，每天售出蛋黄粽子所获得的利润为220元？

查看试题解析
24. 如图，已知菱形 $A B C D$ 的边长为 $2$ ， $∠ A B C = 60 °$ ，点 $M$ 、 $N$ 分别是边 $B C$ 、 $C D$ 上的两个动点， $∠ M A N = 60 °$ ，连接 $M N$ ．

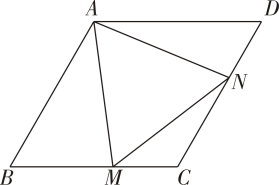(1)、 $△ A M N$ 是等边三角形吗？如是，请证明；如不是，请说明理由．

(2)、在 $M$ 、 $N$ 运动的过程中， $△ C M N$ 的面积存在最大值吗？如存在，请求出该最大值；如不存在，请说明理由．

查看试题解析
25. 已知点 $M (a ， a + 2) (a > 0)$ 在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像上，点 $H (0 ， 1)$ 在 $y$ 轴上，连接 $M H$ ，如图1，将 $M H$ 绕着 $H$ 点顺时针旋转 $90 °$ 至点 $M^{'}$ ，点 $M^{'}$ 正好落在 $x$ 轴上．

(1)、求 $k$ 的值和点 $M^{'}$ 的坐标；

(2)、若点 $P$ 在反比例函数图象上，连接 $H P$ 并延长至点 $E$ ，使得 $P E = P H$ ，连接 $E M^{'}$ 、 $P M^{'}$ ，
①如图2，连接 $M P$ 并延长交 $x$ 轴于点 $Q$ ，当 $P M^{'} ⊥ x$ 轴时，试说明 $E M^{'}$ 平分 $∠ P M^{'} Q$ ；
②如图3，连接 $M M^{'}$ 交 $H E$ 于点 $Q$ ，将 $△ M H M^{'}$ 沿着 $M M^{'}$ 翻折，记点 $H$ 的对应点为 $H^{'}$ ，若点 $H^{'}$ 恰好落在线段 $P E$ 上，求 $△ M^{'} H^{'} E$ 与 $△ P M^{'} Q$ 面积之比．

查看试题解析
26. 已知点 $P (a ， b) (a > b > 0)$ ，过点 $P$ 作 $P A ⊥ y$ 轴于点 $A$ ， $P B ⊥ x$ 伷于点 $B$ ，以 $P$ 为圆心， $P B$ 长为半径作圆交 $P A$ 于点 $C$ ，连接 $O C$ 并延长交 $⊙ P$ 于点 $Q$ ．

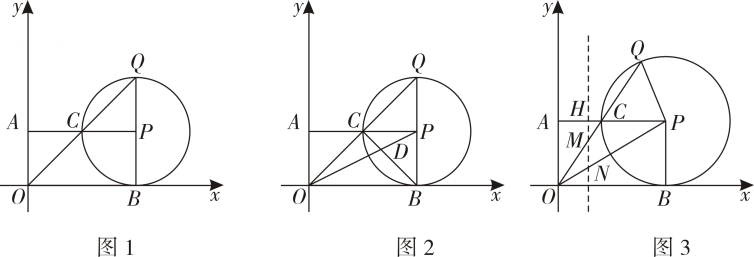(1)、当点 $B$ 、 $P$ 、 $Q$ 在同一条直线上时．
①如图1，点 $C$ 是否为线段 $A P$ 的中点？若是，请证明：若不是，请说明理由．
②如图2，连接 $O P$ 、 $B C$ ，两线交于点 $D$ ，当 $a = 4$ ， $b = 2$ 时，求 $C D$ 的长；

(2)、如图3，点 $M$ 为线段 $O C$ 上一动点，过点 $M$ 作 $y$ 轴的平行线，分别交 $O P$ 、 $A P$ 于点 $N$ 、 $H$ ．若 $\frac{b}{a} = m$ （ $m$ 为定值），试探究在点 $M$ 运动的过程中， $\frac{M N}{A H}$ 的值是否为定值？如果是，请求出这个定值（用含 $m$ 的代数式表示）；如果不是，请说明理由．

查看试题解析