江苏省无锡市宜兴市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式计算正确的是( )A、 B、 C、 D、3. 反比例函数y=-的图象位于( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限4. 下列事件:
2. 下列各式计算正确的是( )A、 B、 C、 D、3. 反比例函数y=-的图象位于( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限4. 下列事件:掷一次骰子,向上一面的点数是;从一个只装有黑色球的袋子摸出一个球,摸到的是白球;个人中至少有两个人的生日是在同一个月份;射击运动员射击一次命中靶心.
其中是确定事件的有( )
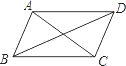
A、个 B、个 C、个 D、个5. 小明和小亮相约到森林公园健身步道上参加健步走活动,他们同时同地出发,线路长度为公里.已知小明的速度是小亮的倍,小明比小亮提前分钟走完全程,设小亮的速度为 , 则下列方程中正确的是( )A、 B、 C、 D、6. 如图,下列条件之一能使平行四边形ABCD是菱形的为( )①AC=BD;②AC⊥BD;③AB=BC;④∠BAD=90°.
 A、①③ B、②③ C、③④ D、①②③7. 若关于的方程无解,则的值为( )A、1 B、1或3 C、1或2 D、2或38. 如图,在矩形中,是的中点,为边上一点,且有连接 , 若 , 则的长为( )
A、①③ B、②③ C、③④ D、①②③7. 若关于的方程无解,则的值为( )A、1 B、1或3 C、1或2 D、2或38. 如图,在矩形中,是的中点,为边上一点,且有连接 , 若 , 则的长为( )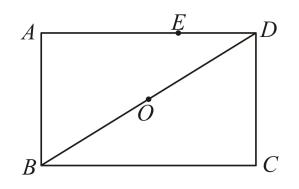 A、 B、 C、 D、9. 如图,在平面直角坐标系中,点在反比例函数的图象上,其纵坐标为 , 过点作轴,交轴于点 , 将线段绕点顺时针旋转得到线段 . 若点也在该反比例函数的图象上,则的值为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,点在反比例函数的图象上,其纵坐标为 , 过点作轴,交轴于点 , 将线段绕点顺时针旋转得到线段 . 若点也在该反比例函数的图象上,则的值为( )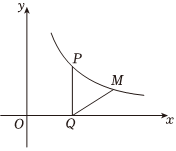 A、 B、 C、 D、10. 如图,在一张菱形纸片中, , , 点在边上不与 , 重合 , 将沿直线折叠得到 , 连接 , , , 有以下四个结论:;;当时,;当平分时,则 . 以上结论中,其中正确的结论个数是( )
A、 B、 C、 D、10. 如图,在一张菱形纸片中, , , 点在边上不与 , 重合 , 将沿直线折叠得到 , 连接 , , , 有以下四个结论:;;当时,;当平分时,则 . 以上结论中,其中正确的结论个数是( )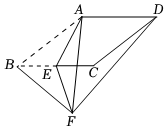 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .
12. 若二次根式 有意义,则x的取值范围是 .13. 某区为了解名初中生的身高情况,抽取了名学生进行身高测量.在这个问题中,样本是 .14. 一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、15、8,则第5组的频率是.15. 有六张形状完全相同不透明的卡片,每张卡片上分别写有 , , , , , , 将无字一面朝上洗匀后,从中任取一张,取到的是无理数的概率是 .16. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.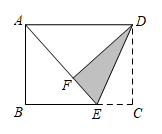 17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点C.点是反比例函数图象上一点且纵坐标是1,连接 , , 则的面积 .
17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点C.点是反比例函数图象上一点且纵坐标是1,连接 , , 则的面积 . 18. 如图,在菱形中, , 折叠该菱形,使点落在边上的点处,折痕分别与边、交于点、当点与点重合时,的长为;当点的位置变化时,长的最大值为 .
18. 如图,在菱形中, , 折叠该菱形,使点落在边上的点处,折痕分别与边、交于点、当点与点重合时,的长为;当点的位置变化时,长的最大值为 .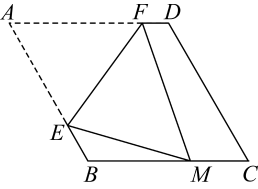
三、解答题
-
19. 为响应全面推进中小学学校“社会主义核心价值观”教育年活动,某校对全校学生进行了中期检测评价,检测结果分为A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如图所示不完整的统计表和统计图.请根据图表提供的信息,解答下列问题:
等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04
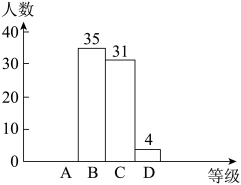 (1)、a= , b=;(2)、请在答题卡上直接补全条形统计图;(3)、若该校共有学生1200人,试估计该校学生在本次检测中达到“C(合格)”或合格以上等级(包括“A(优秀)”和“B(良好)”)的学生人数.20.(1)、(2)、21.(1)、先化简,再求值: , 其中 .(2)、解分式方程: .22. 如图,在中, , 是的中点,是的中点,过点A作交的延长线于点 , 连接 .
(1)、a= , b=;(2)、请在答题卡上直接补全条形统计图;(3)、若该校共有学生1200人,试估计该校学生在本次检测中达到“C(合格)”或合格以上等级(包括“A(优秀)”和“B(良好)”)的学生人数.20.(1)、(2)、21.(1)、先化简,再求值: , 其中 .(2)、解分式方程: .22. 如图,在中, , 是的中点,是的中点,过点A作交的延长线于点 , 连接 .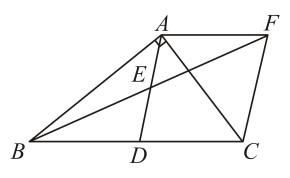 (1)、求证:≌;(2)、证明四边形是菱形.23. 已知 , 按要求完成下列尺规作图不写作法,保留作图痕迹 .
(1)、求证:≌;(2)、证明四边形是菱形.23. 已知 , 按要求完成下列尺规作图不写作法,保留作图痕迹 .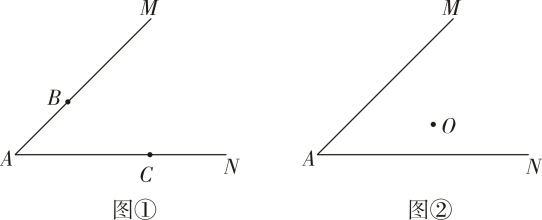 (1)、如图 , , 分别在射线、上,求作;(2)、如图 , 点是内一点,求作线段 , 使、分别在射线、上,且点是的中点.24. 如图,反比例函数的图象与一次函数的图象相交于 , 两点.
(1)、如图 , , 分别在射线、上,求作;(2)、如图 , 点是内一点,求作线段 , 使、分别在射线、上,且点是的中点.24. 如图,反比例函数的图象与一次函数的图象相交于 , 两点.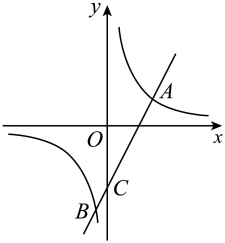 (1)、求反比例函数和一次函数的关系式;(2)、设直线交轴于点 , 点 , 分别在反比例函数和一次函数图象上,若四边形是平行四边形,求点的坐标.25. 某学校图书馆购进甲、乙两种书籍,已知每本甲图书的进价比每本乙图书的进价高元,购买元甲图书的数量与购买元乙图书的数量相同.(1)、求甲、乙两种图书每本的进价分别是多少元?(2)、某中学计划购进甲、乙两种图书共本,且甲种图书的数量比乙种图书的数量至少多本,怎样购买,才能使购书总费用最少?并求出最少费用.26. 在平面直角坐标系中,已知矩形 , 点 , 现将矩形绕点逆时针旋转得到矩形 , 点、、的对应点分别为点、、 .
(1)、求反比例函数和一次函数的关系式;(2)、设直线交轴于点 , 点 , 分别在反比例函数和一次函数图象上,若四边形是平行四边形,求点的坐标.25. 某学校图书馆购进甲、乙两种书籍,已知每本甲图书的进价比每本乙图书的进价高元,购买元甲图书的数量与购买元乙图书的数量相同.(1)、求甲、乙两种图书每本的进价分别是多少元?(2)、某中学计划购进甲、乙两种图书共本,且甲种图书的数量比乙种图书的数量至少多本,怎样购买,才能使购书总费用最少?并求出最少费用.26. 在平面直角坐标系中,已知矩形 , 点 , 现将矩形绕点逆时针旋转得到矩形 , 点、、的对应点分别为点、、 . (1)、如图 , 当点落在边上时,求直线的函数表达式;(2)、如图 , 当、、三点在一直线上时,所在直线与、分别交于点、 , 求线段的长度.(3)、如图 , 设点为边的中点,连接 , 在矩形旋转过程中,点到直线的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.
(1)、如图 , 当点落在边上时,求直线的函数表达式;(2)、如图 , 当、、三点在一直线上时,所在直线与、分别交于点、 , 求线段的长度.(3)、如图 , 设点为边的中点,连接 , 在矩形旋转过程中,点到直线的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.