江苏省泰州市靖江市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 2023年暑假即将来临,我国各大博物院(馆)是同学们不错的选择,下面四幅图是我国一些博物院(馆)的标志,其中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 利用公式法求解可得一元二次方程式的两解为、 , 且 , 求a值为何( )A、 B、 C、 D、4. 彩民小明购买10000张彩票,中一等奖.这个事件是( )A、必然事件 B、确定性事件 C、不可能事件 D、随机事件5. 下列四个命题中不正确的是( )A、有两边相等的平行四边形是菱形 B、一组邻边相等的矩形是正方形 C、对角线相等的平行四边形是矩形 D、对角互补的平行四边形是矩形6. 探究函数的图像发现,可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据以上信息判断,下列直线中与函数的图像没有公共点的是( )A、经过点且平行于x轴的直线 B、经过点且平行于x轴的直线 C、经过点且平行于y轴的直线 D、经过点且平行于y轴的直线
2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 利用公式法求解可得一元二次方程式的两解为、 , 且 , 求a值为何( )A、 B、 C、 D、4. 彩民小明购买10000张彩票,中一等奖.这个事件是( )A、必然事件 B、确定性事件 C、不可能事件 D、随机事件5. 下列四个命题中不正确的是( )A、有两边相等的平行四边形是菱形 B、一组邻边相等的矩形是正方形 C、对角线相等的平行四边形是矩形 D、对角互补的平行四边形是矩形6. 探究函数的图像发现,可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据以上信息判断,下列直线中与函数的图像没有公共点的是( )A、经过点且平行于x轴的直线 B、经过点且平行于x轴的直线 C、经过点且平行于y轴的直线 D、经过点且平行于y轴的直线二、填空题
-
7. 若式子有意义,则x的取值范围是8. 某中学数学教研组有32名教师,将他们按年龄分组,在38-45岁组内的教师有8名教师,那么这个小组的频率是 .9. 若实数a、b在数轴上对应点的位置如图所示,则化简的结果是 .
 10. 已知n为整数,当时,分式的值是整数.11. 如图是反比例函数的图象,则的值可能是.(写出一个可能的值即可).
10. 已知n为整数,当时,分式的值是整数.11. 如图是反比例函数的图象,则的值可能是.(写出一个可能的值即可). 12. 解关于的方程有增根,则的值为13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .
12. 解关于的方程有增根,则的值为13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .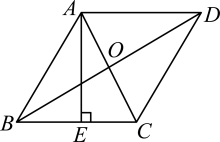 14. 如图,在矩形中,E为的中点,F为上一点,将沿折叠,点A恰好落在上的点G处.若 , 则折痕的长为 .
14. 如图,在矩形中,E为的中点,F为上一点,将沿折叠,点A恰好落在上的点G处.若 , 则折痕的长为 . 15. 如图,在矩形中, , F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= .
15. 如图,在矩形中, , F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= . 16. 如图,在中, , , . 将绕点C按顺时针方向旋转后得 , 直线、相交于点 . 取的中点 , 连接 , 则长的最大值为 .
16. 如图,在中, , , . 将绕点C按顺时针方向旋转后得 , 直线、相交于点 . 取的中点 , 连接 , 则长的最大值为 .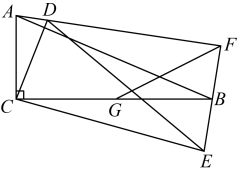
三、解答题
-
17. 计算:(1)、;(2)、 .18. 解下列方程:(1)、;(2)、 .19. 已知关于x的一元二次方程有两个不相等的实数根、 .(1)、求k的取值范围;(2)、若 (填序号),求k的值.(从①x1•x2=2;②x1+x2=3;③x1-x2=1中选择一个作为条件,补充完整题目,并完成解答.)20. 小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:

根据上述三个统计图,请解答:
(1)、2014~2019年三种品牌电视机销售总量最多的是品牌,月平均销售量最稳定的是品牌。(2)、2019年其他品牌的电视机年销售总量是多少万台?(3)、货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由。21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.的顶点均在格点,点D为上一格点,点E为上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.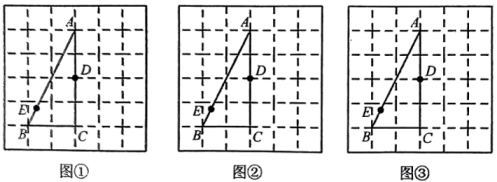 (1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .22. 如图,已知平行四边形中,对角线交点O,E是延长线上的点,且是等边三角形.
(1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .22. 如图,已知平行四边形中,对角线交点O,E是延长线上的点,且是等边三角形. (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.23. 在春季,很多学校会组织学生进行春游.某校组织学生到离学校有90公里的生态园春游,队伍8:00从学校坐大巴车出发.李老师因有事情,8:30从学校自驾小车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前15分钟到达生态园.求大巴车与小车的平均速度.24. 实验数据显示,一般情况下,成人喝低度白酒后,小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;小时后(包括小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.23. 在春季,很多学校会组织学生进行春游.某校组织学生到离学校有90公里的生态园春游,队伍8:00从学校坐大巴车出发.李老师因有事情,8:30从学校自驾小车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前15分钟到达生态园.求大巴车与小车的平均速度.24. 实验数据显示,一般情况下,成人喝低度白酒后,小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;小时后(包括小时)y与x成反比例.根据图中提供的信息,解答下列问题: (1)、写出一般情况下,成人喝低度白酒后,y与x之间的函数关系式及相应的自变量取值范围.(2)、按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完低度白酒,第二天早上7:00能否驾车去上班?请说明理由.25. 数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图所示的长方形纸条 , 其中 , . 然后在纸条上任意画一条线段 , 将纸片沿折叠,与交于点 , 得到 . 如图所示:
(1)、写出一般情况下,成人喝低度白酒后,y与x之间的函数关系式及相应的自变量取值范围.(2)、按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完低度白酒,第二天早上7:00能否驾车去上班?请说明理由.25. 数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图所示的长方形纸条 , 其中 , . 然后在纸条上任意画一条线段 , 将纸片沿折叠,与交于点 , 得到 . 如图所示: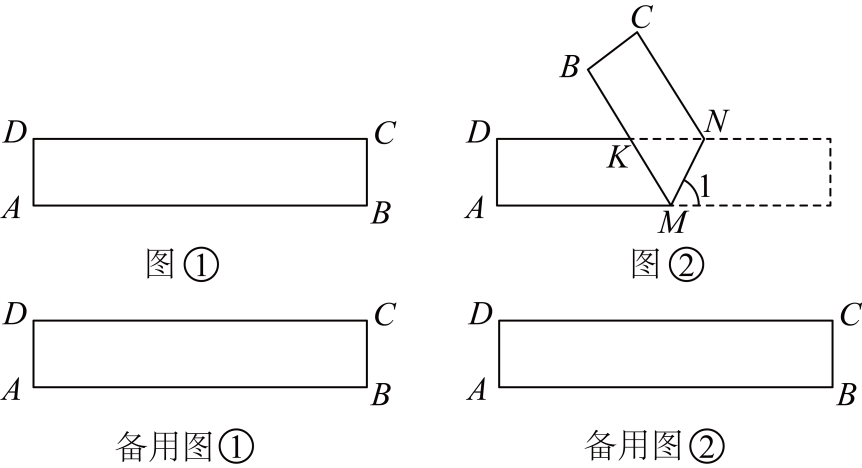 (1)、【基础回顾】在图中,若 , ∠MKN=°;(直接写出答案)(2)、【操作探究】改变折痕位置,始终是 三角形,请说明理由;(3)、爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为 , 此时的大小可以为;(4)、【拓展延伸】小明继续动手操作进行折纸,发现了面积存在最大值,请你求出这个最大值.26. 在学习反比例函数后,小华在同一个平面直角坐标系中画出了和的图像,两个函数图象交于两点,在线段上选取一点P,过点P作y轴的平行线交反比例函数图象于点Q(如图1),在点P移动的过程中,发现的长度随着点P的运动而变化.为了进一步研究的长度与点P的横坐标之间的关系,小华提出了下列问题:
(1)、【基础回顾】在图中,若 , ∠MKN=°;(直接写出答案)(2)、【操作探究】改变折痕位置,始终是 三角形,请说明理由;(3)、爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为 , 此时的大小可以为;(4)、【拓展延伸】小明继续动手操作进行折纸,发现了面积存在最大值,请你求出这个最大值.26. 在学习反比例函数后,小华在同一个平面直角坐标系中画出了和的图像,两个函数图象交于两点,在线段上选取一点P,过点P作y轴的平行线交反比例函数图象于点Q(如图1),在点P移动的过程中,发现的长度随着点P的运动而变化.为了进一步研究的长度与点P的横坐标之间的关系,小华提出了下列问题: (1)、设点P的横坐标为x,的长度为y,则y与x之间的函数关系式为;(2)、为了进一步研究(1)中的函数关系,决定运用列表,描点,连线的方法绘制函数的图象:
(1)、设点P的横坐标为x,的长度为y,则y与x之间的函数关系式为;(2)、为了进一步研究(1)中的函数关系,决定运用列表,描点,连线的方法绘制函数的图象:①列表:
x
1
2
3
4
6
9
y
0
m
4
n
0
表中m= ▲ , n= ▲ ;
②描点:根据上表中的数据,在图2中描出各点;
③连线:请在图2中画出该函数的图象.观察函数图象,当 ▲ 时,y的最大值为 ▲ .
(3)、①已知某矩形的一组邻边长分别为m,n,且该矩形的周长W与n存在函数关系 , 求m取最大值时矩形的对角线长.②如图3,在平面直角坐标系中,直线与坐标轴分别交于点A、B,点M为反比例函数上的任意一点,过点M作轴于点C,轴于点D.求四边形面积的最小值.