陕西省西安市长安区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm2. 下列各图中,作△ABC边AC上的高,正确的是( )A、
 B、
B、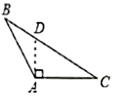 C、
C、 D、
D、 3. 一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,4,5,6六个数字,抛掷这枚骰子一次,则向上的面的数字大于4的概率是( )A、 B、 C、 D、4. 下面的图形是用数学家名字命名的,其中轴对称图形的个数是( )
3. 一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,4,5,6六个数字,抛掷这枚骰子一次,则向上的面的数字大于4的概率是( )A、 B、 C、 D、4. 下面的图形是用数学家名字命名的,其中轴对称图形的个数是( ) A、4 B、3 C、2 D、15. 在 ABC中, A: B: C=2:3:5,则 ABC是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、不能确定6. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球7. 如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( )
A、4 B、3 C、2 D、15. 在 ABC中, A: B: C=2:3:5,则 ABC是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、不能确定6. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球7. 如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( ) A、∠A=∠D B、AB=DE C、AC∥DF D、AC=DF8. 一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小红为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小红共摸了1000次,其中有202次摸到白球,因此小红估计口袋中的红球有( )A、60个 B、50个 C、40个 D、30个9. 下列说法中,错误的是( )A、对顶角相等 B、三角形的三条角平分线一定交于一点 C、a、b、c是同一平面内的三条直线,如果 , , 那么 D、a、b、c是同一平面内的三条直线,如果 , 那么10. 如图,在长方形的中,已知 , , 点以的速度由点向点运动,同时点以的速度由点向点运动,若以 , , 为顶点的三角形和以 , , 为顶点的三角形全等,则的值为( )
A、∠A=∠D B、AB=DE C、AC∥DF D、AC=DF8. 一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小红为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小红共摸了1000次,其中有202次摸到白球,因此小红估计口袋中的红球有( )A、60个 B、50个 C、40个 D、30个9. 下列说法中,错误的是( )A、对顶角相等 B、三角形的三条角平分线一定交于一点 C、a、b、c是同一平面内的三条直线,如果 , , 那么 D、a、b、c是同一平面内的三条直线,如果 , 那么10. 如图,在长方形的中,已知 , , 点以的速度由点向点运动,同时点以的速度由点向点运动,若以 , , 为顶点的三角形和以 , , 为顶点的三角形全等,则的值为( ) A、2 B、3 C、2或 D、2或
A、2 B、3 C、2或 D、2或二、填空题
-
11. 如图是一个4×4的方格,若在这个方格内投掷飞镖,则飞镖恰好落在阴影部分的概率是 .
 12. 将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为度.
12. 将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=20°,则∠DBC为度. 13. 如图,直线 , , 则的度数为 .
13. 如图,直线 , , 则的度数为 . 14. 如图,在内有一点O到三个顶点的距离相等,连接 . 若 , 则的度数为 .
14. 如图,在内有一点O到三个顶点的距离相等,连接 . 若 , 则的度数为 . 15. 若 , 则 .16. 如图,D是延长线上一点,交于点E, , . 若 , , 则的长是 .
15. 若 , 则 .16. 如图,D是延长线上一点,交于点E, , . 若 , , 则的长是 . 17. 如图, , 是线段的垂直平分线,垂足为点D,的平分线交于点E,连接 , 则的度数是 .
17. 如图, , 是线段的垂直平分线,垂足为点D,的平分线交于点E,连接 , 则的度数是 . 18. 如图,有一块边长为6的正方形塑料模板 , 将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与交于点F,与延长线交于点E,则四边形的面积是 .
18. 如图,有一块边长为6的正方形塑料模板 , 将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与交于点F,与延长线交于点E,则四边形的面积是 .
三、解答题
-
19. 计算:(1)、(2)、20. 作图题(保留作图痕迹,不写作法)
 (1)、如图1,网格中有一个格点△ABC(即三角形的顶点都在格点上),画出交于直线MN的对称图形;(2)、如图2,在中, , 用尺规作出对称轴l.21. 如图,已知 , 平分 , . 你在横线上补充其推理过程或理由.
(1)、如图1,网格中有一个格点△ABC(即三角形的顶点都在格点上),画出交于直线MN的对称图形;(2)、如图2,在中, , 用尺规作出对称轴l.21. 如图,已知 , 平分 , . 你在横线上补充其推理过程或理由. (1)、与有怎样的位置关系?请说明理由;
(1)、与有怎样的位置关系?请说明理由;.
理由:因为(已知),
所以 ▲ (理由: ),
因为(已知),
所以 ▲ (等量代换)
所以(理由: ).
(2)、若 , 求的度数.因为平分(已知),
所以 ▲ (角平分线定义),
由(1)知 ,
所以(等量代换),
因为 ▲ (三角形内角和定理),
所以 ▲ (等式的性质).
22. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),如图所示.并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会,转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.小红和妈妈购买了168元的商品,请你分析计算:颜色
奖品
红色
玩具熊
黄色
童话书
绿色
彩笔
 (1)、小红获得童话书的概率是多少?(2)、小红获得奖品的概率是多少?23. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ),点 在 上,点 和 分别与木墙的顶端重合.
(1)、小红获得童话书的概率是多少?(2)、小红获得奖品的概率是多少?23. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ),点 在 上,点 和 分别与木墙的顶端重合.
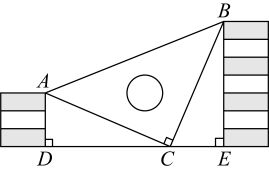 (1)、求证: ;(2)、求两堵木墙之间的距离.24. 甲、乙两人匀速步行从新华书店沿笔直的公路到某公园游玩,先到公园门口的人原地休息,从书店到公园门口共 , 已知甲先出发 . 在整个步行过程中,甲、乙两人的距离与甲出发的时间之间的关系如图所示.
(1)、求证: ;(2)、求两堵木墙之间的距离.24. 甲、乙两人匀速步行从新华书店沿笔直的公路到某公园游玩,先到公园门口的人原地休息,从书店到公园门口共 , 已知甲先出发 . 在整个步行过程中,甲、乙两人的距离与甲出发的时间之间的关系如图所示. (1)、甲步行的速度是多少?(2)、乙步行的速度是多少?(3)、甲、乙两人相距最远是多少?(4)、求乙从书店出发到追上甲这个过程中,与甲出发的时间之间的解析式.
(1)、甲步行的速度是多少?(2)、乙步行的速度是多少?(3)、甲、乙两人相距最远是多少?(4)、求乙从书店出发到追上甲这个过程中,与甲出发的时间之间的解析式.