陕西省延安市志丹县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列是最简二次根式的是( )A、 B、 C、 D、2. 以下列各组数为边长,能构成直角三角形的是( )A、 B、 C、 D、3. 点A(1,m)在函数y=2x的图象上,则m的值是( )A、2 B、1 C、0.5 D、4. 如图,在菱形中,对角线 , 相交于点 , 添加下列条件,能使菱形成为正方形的是( )
 A、 B、 C、 D、平分5. 下列计算正确的是( )A、 B、 C、 D、6. 已知一组数据: , 它们的平均数是6,则这组数据的众数是( )A、6 B、2 C、8 D、77. 在平面直角坐标系中,将一次函数的图象向左平移3个单位长度后经过点 , 则的值为( )A、 B、2 C、 D、48. 已知在平行四边形中, , E是上一点,的周长是平行四边形周长的一半,且 , 、交于点O,连接 , 则的长为( )
A、 B、 C、 D、平分5. 下列计算正确的是( )A、 B、 C、 D、6. 已知一组数据: , 它们的平均数是6,则这组数据的众数是( )A、6 B、2 C、8 D、77. 在平面直角坐标系中,将一次函数的图象向左平移3个单位长度后经过点 , 则的值为( )A、 B、2 C、 D、48. 已知在平行四边形中, , E是上一点,的周长是平行四边形周长的一半,且 , 、交于点O,连接 , 则的长为( ) A、3 B、5 C、 D、
A、3 B、5 C、 D、二、填空题
-
9. 比较大小:2(填“>”“<”或“=”)10. 甲、乙两人进行射击测试,每人10次射击的平均数都是8环,方差分别为 , , 则成绩最稳定的是 .11. 勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”.即(a为勾,b为股,c为弦),若“勾”为2,“股”为3,则“弦”是 .12. 平行四边形在平面直角坐标系中的位置如图所示, , 则点的坐标为 .
 13. 在直角坐标系中,点 , 的坐标分别为 , , 在轴上找一点 , 使得的周长最小,则点的坐标为 .
13. 在直角坐标系中,点 , 的坐标分别为 , , 在轴上找一点 , 使得的周长最小,则点的坐标为 .三、解答题
-
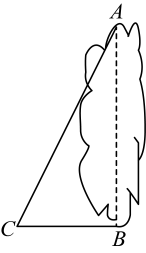
14. 计算: .15. 已知正比例函数经过点 , 求的值.16. 如图,湖的两岸有两棵景观树,在与垂直的方向上取一点 , 测得米,米.求两棵景观树之间的距离.
 17. 请在数轴上用尺规作出所对应的点.(保留作图痕迹,不写作法)
17. 请在数轴上用尺规作出所对应的点.(保留作图痕迹,不写作法) 18. 已知:如图,四边形是平行四边形,P,Q是对角线上的两个点,且 . 求证: .
18. 已知:如图,四边形是平行四边形,P,Q是对角线上的两个点,且 . 求证: . 19. 某校八(1)班次数学测验(卷面满分 分)成绩统计,有 的优生,他们的人均分为 分, 的不及格,他们的人均分为 分,其它同学的人均分为 分,求全班这次测试成绩的平均分.20. 如图,矩形纸片中, , 将沿折叠,使点落在点处,交于点 , 求的长.
19. 某校八(1)班次数学测验(卷面满分 分)成绩统计,有 的优生,他们的人均分为 分, 的不及格,他们的人均分为 分,其它同学的人均分为 分,求全班这次测试成绩的平均分.20. 如图,矩形纸片中, , 将沿折叠,使点落在点处,交于点 , 求的长. 21. 2022年10月12日,“天宫课堂”第三课开讲.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),组: , 组: , 组: , 组: , 组: , 并绘制了如下不完整的统计图.
21. 2022年10月12日,“天宫课堂”第三课开讲.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),组: , 组: , 组: , 组: , 组: , 并绘制了如下不完整的统计图.
请结合统计图,解答下列问题:
(1)、本次调查一共随机抽取了名学生的成绩;(2)、频数分布直方图中 , 所抽取学生成绩的中位数落在 组,并补全学生成绩频数分布直方图;(3)、若成绩在90分及以上为优秀,学校共有4500名学生,估计该校成绩优秀的学生有多少名?22. 如图,等边的边长是4,D、E分别为、的中点,过E点作交的延长线于点F,连接 . (1)、求证:四边形平行四边形;(2)、求的长.23. 直线交轴于点 , 交轴于点 , 点与点关于轴对称,点与点关于轴对称.(1)、求点的坐标;(2)、求直线对应的函数解析式.24. 如图,在四边形中, , , 对角线交于点O,平分 , 过点C作交的延长线于点E,连接 .
(1)、求证:四边形平行四边形;(2)、求的长.23. 直线交轴于点 , 交轴于点 , 点与点关于轴对称,点与点关于轴对称.(1)、求点的坐标;(2)、求直线对应的函数解析式.24. 如图,在四边形中, , , 对角线交于点O,平分 , 过点C作交的延长线于点E,连接 . (1)、求证:四边形是菱形;(2)、若 , , 求的长.
(1)、求证:四边形是菱形;(2)、若 , , 求的长.
