陕西省榆林市定边县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列是各地的地铁标志,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是随机事件的是( )A、钝角三角形的内角和大于 B、雨后会出现彩虹 C、在只放红、白小球的盒子中摸出黄球 D、妹妹的年龄比姐姐的年龄小3. 下列各项中,两个图形属于全等图形的是( )A、
2. 下列事件中,是随机事件的是( )A、钝角三角形的内角和大于 B、雨后会出现彩虹 C、在只放红、白小球的盒子中摸出黄球 D、妹妹的年龄比姐姐的年龄小3. 下列各项中,两个图形属于全等图形的是( )A、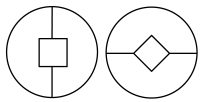 B、
B、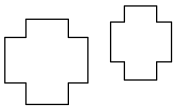 C、
C、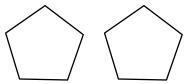 D、
D、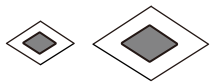 4. 星载原子钟是卫星导航系统的“心脏”,对系统定位和授时精度具有决定性作用.“北斗”三号卫星导航系统装载国产高精度星载原子钟,保证“北斗”优于20纳秒的授时精度. 1纳秒秒,那么20纳秒用科学记数法表示应为( )A、秒 B、秒 C、秒 D、秒5. 下列运算中,正确的是( )A、 B、 C、 D、6. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种7. 周末,乐乐去公园游玩,坐上了他向往已久的摩天轮(如图所示).摩天轮上,乐乐离地面的高度h(米)和他坐上摩天轮后旋转的时间t(分)之间的部分关系图象如图所示,下列说法错误的是( )
4. 星载原子钟是卫星导航系统的“心脏”,对系统定位和授时精度具有决定性作用.“北斗”三号卫星导航系统装载国产高精度星载原子钟,保证“北斗”优于20纳秒的授时精度. 1纳秒秒,那么20纳秒用科学记数法表示应为( )A、秒 B、秒 C、秒 D、秒5. 下列运算中,正确的是( )A、 B、 C、 D、6. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种7. 周末,乐乐去公园游玩,坐上了他向往已久的摩天轮(如图所示).摩天轮上,乐乐离地面的高度h(米)和他坐上摩天轮后旋转的时间t(分)之间的部分关系图象如图所示,下列说法错误的是( ) A、摩天轮转动6分钟后,离地面的高度为3米 B、摩天轮转动的第3分钟和第9分钟,离地面的高度相同 C、摩天轮转动一周需要6分钟 D、乐乐离地面的最大高度是42米8. 如图,直线 , 点在上,点在上,平分交于点 , , 已知 , 则的度数为( )
A、摩天轮转动6分钟后,离地面的高度为3米 B、摩天轮转动的第3分钟和第9分钟,离地面的高度相同 C、摩天轮转动一周需要6分钟 D、乐乐离地面的最大高度是42米8. 如图,直线 , 点在上,点在上,平分交于点 , , 已知 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知等腰三角形的顶角的度数为108°,则底角的度数为 .10. 如图,在和中,点在同一条直线上,且 , 请你再添加一个条件: , 使得 .
 11. 已知 , 则的值是 .12. 如图,用灰、白两种颜色的正六边形镶嵌成若干图案,按照这种规律,第n个图案中白色正六边形的个数y与n之间的关系式为 .
11. 已知 , 则的值是 .12. 如图,用灰、白两种颜色的正六边形镶嵌成若干图案,按照这种规律,第n个图案中白色正六边形的个数y与n之间的关系式为 .
三、解答题
-
13. 计算: .14. 对某批KN95口罩的质量进行随机抽查,结果如下表所示:
随机抽取的口罩数
100
200
400
600
800
1200
合格数
98
197
391
588
785
1176
合格的频率
0.980
(1)、完成上表;(保留三位小数)(2)、根据上表,在这批口罩中任取一个,它是合格的概率大约是 . (精确到0.01)15. 已知 , 求代数式的值.16. 已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF平行吗?为什么? 17. 如图,已知四边形 , 连接 , 请用尺规作图法在边上找一点P,使得与的面积相等.(不写作法,保留作图痕迹)
17. 如图,已知四边形 , 连接 , 请用尺规作图法在边上找一点P,使得与的面积相等.(不写作法,保留作图痕迹) 18. 如图所示,O为码头,A,B两个灯塔与码头的距离相等, , 为海岸线,一轮船从码头开出,计划沿的平分线航行,航行途中,某时测得船所在的位置C与灯塔A,B的距离相等,此时轮船有没有偏离航线?并说明你的理由.
18. 如图所示,O为码头,A,B两个灯塔与码头的距离相等, , 为海岸线,一轮船从码头开出,计划沿的平分线航行,航行途中,某时测得船所在的位置C与灯塔A,B的距离相等,此时轮船有没有偏离航线?并说明你的理由. 19. 某商场在“6.18”期间大力促销,通过降低售价,增加销售量的方法来提高利润.某商品原价为80元,随着不同幅度的降价,日销量(件)发生的变化如下表所示().
19. 某商场在“6.18”期间大力促销,通过降低售价,增加销售量的方法来提高利润.某商品原价为80元,随着不同幅度的降价,日销量(件)发生的变化如下表所示().降价金额元
0
1
2
3
4
5
6
日销量件
660
680
700
720
740
760
780
(1)、上表中,是自变量,是因变量;(2)、根据表中数据,求出售价为70元时,日销量的件数.20. 如图,在中,垂直平分 , 分别交于点平分 . (1)、求的度数;(2)、若 , 求的长.21. 阅读材料:下面是底数大于1的数比较大小的两种方法:
(1)、求的度数;(2)、若 , 求的长.21. 阅读材料:下面是底数大于1的数比较大小的两种方法:①比较 , 的大小:当时, , 所以当同底数时,指数越大,值越大;
②比较和的大小:因为 , , 所以 .
可以将其先化为同指数,再比较大小,所以同指数时,底数越大,值越大.
根据上述材料,解答下列问题:
(1)、比较大小:(填“”或“”)(2)、已知 , , , 试比较 , , 的大小.22. 如图,是的边上的中线,点在上,若与相等吗?为什么? 23. 乐乐从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买文具,于是又折回到刚经过的文具店,买到文具后继续骑车去学校.如图是他本次上学所用的时间与离家的距离之间的关系图.根据图中提供的信息,解答下列问题:
23. 乐乐从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买文具,于是又折回到刚经过的文具店,买到文具后继续骑车去学校.如图是他本次上学所用的时间与离家的距离之间的关系图.根据图中提供的信息,解答下列问题: (1)、乐乐在文具店停留了分钟,文具店到学校的距离是米;(2)、在整个上学途中,哪个时间段乐乐骑车速度最快?最快的速度是多少?(3)、如果乐乐不买文具,以往常的速度去学校,需要多长时间?
(1)、乐乐在文具店停留了分钟,文具店到学校的距离是米;(2)、在整个上学途中,哪个时间段乐乐骑车速度最快?最快的速度是多少?(3)、如果乐乐不买文具,以往常的速度去学校,需要多长时间?

