陕西省榆林市子洲县2022-2023学年七年级下学期6月期末
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 古语有云“滴水石穿”,若水珠不断滴在一块石头上,石头上会形成一个深为的小坑.将数据用科学记数法表示正确的是( )A、 B、 C、 D、2. 中华姓氏源于上古,每个姓氏都有自己的图腾.下列姓氏图腾是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片 B、中秋节晚上能看到月亮 C、买100张彩票一定会中奖 D、在只装有红球的袋中摸出1个球是红球4. 如图,直线 , 的顶点B在直线上,若 , 则的度数为( )
3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片 B、中秋节晚上能看到月亮 C、买100张彩票一定会中奖 D、在只装有红球的袋中摸出1个球是红球4. 如图,直线 , 的顶点B在直线上,若 , 则的度数为( )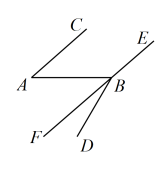 A、100° B、120° C、140° D、160°5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( )
A、100° B、120° C、140° D、160°5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( ) A、 B、 C、 D、7. 小丽从家里出发去超市购物,购物完后从超市返回家中,小丽离家的路程y(米)和所经过的时间x(分)之间的关系如图所示,则下列说法错误的是( )
A、 B、 C、 D、7. 小丽从家里出发去超市购物,购物完后从超市返回家中,小丽离家的路程y(米)和所经过的时间x(分)之间的关系如图所示,则下列说法错误的是( )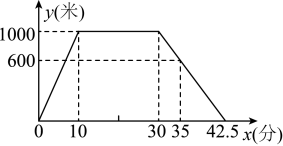 A、小丽家到超市的路程是1000米 B、小丽在超市购物用时20分钟 C、当时,小丽离家的路程是600米 D、小丽购物完从超市回到家用时分钟8. 如图,在中,D,E是边上的两点, , 则的度数为( )
A、小丽家到超市的路程是1000米 B、小丽在超市购物用时20分钟 C、当时,小丽离家的路程是600米 D、小丽购物完从超市回到家用时分钟8. 如图,在中,D,E是边上的两点, , 则的度数为( ) A、90° B、80° C、70° D、60°
A、90° B、80° C、70° D、60°二、填空题
-
9. 如图,要使CDBE , 需要添加的一个条件为: .
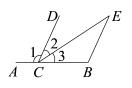 10. 一个不透明的盒子中装有个除颜色外无其他差别的小球,其中有个黄球和个绿球,其余都是红球,从中随机摸出一个小球,恰好是红球的概率为 .11. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 .
10. 一个不透明的盒子中装有个除颜色外无其他差别的小球,其中有个黄球和个绿球,其余都是红球,从中随机摸出一个小球,恰好是红球的概率为 .11. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 . 12. 下面的表格列出了一个实验室的部分统计数据,表示皮球从高处落下时,弹跳高度(厘米)与下降高度(厘米)的关系:
12. 下面的表格列出了一个实验室的部分统计数据,表示皮球从高处落下时,弹跳高度(厘米)与下降高度(厘米)的关系:(厘米)
…
…
(厘米)
…
…
根据表格中两个变量之间的关系,则当时, .
13. 如图所示,在中,点E是边上一点,且 , 点D在上,连接 , , 若 , , , 则的度数为°.
三、解答题
-
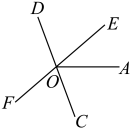
14. 计算: .15. 如图,直线与交于点O,平分 , 若 , 求的度数.
 16. 某足球运动员在同一条件下进行射门,结果如表所示:
16. 某足球运动员在同一条件下进行射门,结果如表所示:射门次数n
20
50
100
200
500
800
踢进球门的频数m
13
a
58
104
255
400
踢进球门的频率
b
根据表格中的数据解答下列问题:
(1)、填空: , ;(2)、这名足球运动员在同一条件下再射门一次,估计他踢进球门的概率(结果精确到)17. 如图,已知 , 利用尺规作图法求作边的中线 . (不写作法,保留作图痕迹) 18. 如图,在中, , 延长至 , 使得 , 连接 , 再延长至 , 使得 , 连接 . 求证: .
18. 如图,在中, , 延长至 , 使得 , 连接 , 再延长至 , 使得 , 连接 . 求证: . 19. 如图,以直线l为对称轴在网格中画出图形的另一半.
19. 如图,以直线l为对称轴在网格中画出图形的另一半. 20. 先化简,再求值: , 其中 , .21. 如图,、两建筑物位于河的两岸,要测得它们之间的距离,可以从点出发沿河岸画一条射线 , 在上截取 , 过作 , 使点、、在同一直线上,则的长就是、之间的距离,请你说明理由.
20. 先化简,再求值: , 其中 , .21. 如图,、两建筑物位于河的两岸,要测得它们之间的距离,可以从点出发沿河岸画一条射线 , 在上截取 , 过作 , 使点、、在同一直线上,则的长就是、之间的距离,请你说明理由.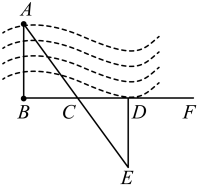 22. 如图,已知点E、F在直线上,点G在线段上,连接与交于点H,已知 , , 若 , , 求的度数.
22. 如图,已知点E、F在直线上,点G在线段上,连接与交于点H,已知 , , 若 , , 求的度数. 23. 用100米长的篱笆在地上围成一个长方形,当长方形的宽由小到大变化时,长方形的面积也随之发生变化.设长方形的宽为x(米),长方形的面积为y(平方米).(1)、在这个变化过程中,自变量是 , 因变量是;(2)、求长方形的面积y(平方米)与长方形的宽x(米)之间的关系式:(3)、当长方形的宽由1米变化到20米时,长方形面积由(平方米)变化到(平方米),求和的值.24. 如图,点P在内部,点P关于、对称的点分别为C、D,连接交于点R,连接交于点T,连接 , 交于点M,交于点N,连接、 .
23. 用100米长的篱笆在地上围成一个长方形,当长方形的宽由小到大变化时,长方形的面积也随之发生变化.设长方形的宽为x(米),长方形的面积为y(平方米).(1)、在这个变化过程中,自变量是 , 因变量是;(2)、求长方形的面积y(平方米)与长方形的宽x(米)之间的关系式:(3)、当长方形的宽由1米变化到20米时,长方形面积由(平方米)变化到(平方米),求和的值.24. 如图,点P在内部,点P关于、对称的点分别为C、D,连接交于点R,连接交于点T,连接 , 交于点M,交于点N,连接、 .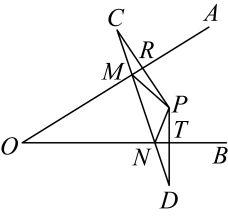 (1)、若 , 求的周长;(2)、若 , , 求的度数.25. 在学习过“概率”之后,张老师要评价学生们的学习效果,他设计了一个转盘,并将其均匀分成6份,分别标上1,2,3,4,5,6这六个数字,转动转盘,转盘停止时,指针所指向的数字即为转出的数.张老师让同学们自己提出问题,下面是三位同学的问题,请你帮助解答.(1)、小颖:转动转盘,转出的数字为6的概率是;(2)、小琪:转动转盘,转出的数字小于3的概率是;(3)、小乐拿了两张分别写有数字4,5的卡片,随机转动转盘,停止后记下指针指向的数字,与卡片上的数字分别作为三条线段的长度,这三条线段能构成三角形的概率是 .26. 【问题背景】
(1)、若 , 求的周长;(2)、若 , , 求的度数.25. 在学习过“概率”之后,张老师要评价学生们的学习效果,他设计了一个转盘,并将其均匀分成6份,分别标上1,2,3,4,5,6这六个数字,转动转盘,转盘停止时,指针所指向的数字即为转出的数.张老师让同学们自己提出问题,下面是三位同学的问题,请你帮助解答.(1)、小颖:转动转盘,转出的数字为6的概率是;(2)、小琪:转动转盘,转出的数字小于3的概率是;(3)、小乐拿了两张分别写有数字4,5的卡片,随机转动转盘,停止后记下指针指向的数字,与卡片上的数字分别作为三条线段的长度,这三条线段能构成三角形的概率是 .26. 【问题背景】如图, . 连接 , 点E,F在上,且 , 连接 , 且 .
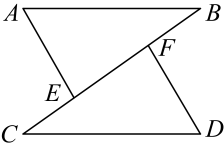
【问题探究】
(1)、试说明::(2)、若 ,①试判断的形状,并说明理由:
②若 , 求的度数.